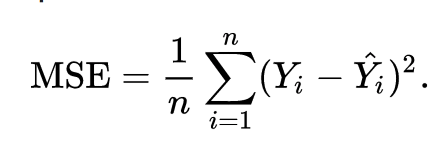ИТ Блог. Администрирование серверов на основе Linux (Ubuntu, Debian, CentOS, openSUSE)
Хотя машинное обучение не ново, сейчас данных больше, чем когда-либо прежде, что способствует его популярности в последнее время. Мы рассмотрим два популярных алгоритма машинного обучения: линейную регрессию и логистическую регрессию с математикой и реализацией.
Линейная регрессия — это простой, но эффективный алгоритм машинного обучения с учителем для прогнозирования непрерывных переменных. Линейная регрессия пытается определить, как входная переменная (независимая переменная) отличается от выходной переменной (переменная ответа). Многие продвинутые алгоритмы контролируемого машинного обучения основаны на концепциях линейной регрессии. Линейная регрессия обычно используется в задачах машинного обучения для прогнозирования непрерывных переменных, в которых целевые и функциональные переменные имеют линейную связь.
Ниже приведены основные компоненты простой линейной регрессии: выполняются непрерывная входная переменная, переменная непрерывного отклика и допущения линейной регрессии.
Модель линейной регрессии пытается подобрать линию, которая проходит через наиболее значительное количество точек, при этом минимизируя квадрат расстояния (функция стоимости) точек до значений подобранной линии с учетом набора входных точек данных (x) и откликов (y).
В результате функция затрат в конечном итоге сводится к минимуму. Функция стоимости для линейной регрессии обычно представляет собой среднеквадратичную ошибку :
Уравнение регрессии записывается как y = β1x + βo.
Член c представляет точку пересечения, m представляет наклон линии регрессии, x представляет входную переменную, а y представляет прогнозируемое значение переменной ответа.
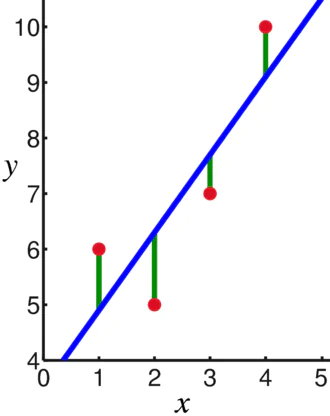
Из базовой математики мы знаем, что прямая линия определяется двумя параметрами: наклоном и пересечением. Алгоритм линейной регрессии выбирает некоторые начальные параметры и постоянно обновляет их, чтобы минимизировать стандартное отклонение. Ниже приведено изображение, показывающее линию регрессии (синий), отклонения (зеленый) и точки данных (красный).
Линейная регрессия также может быть расширена на несколько входных переменных, и подход остается точно таким же. Уравнение линии для нескольких переменных представлено следующим образом:
Давайте спрогнозируем целевую переменную, используя единственную входную переменную. Приведенный ниже пример и набор данных взяты из официальной документации scikit-learn . scikit-learn — широко используемая библиотека для разработки моделей машинного обучения.
import matplotlib.pyplot as plt
import numpy as
# Разделите данные на обучающие/тестовые наборы
diabetes_X_train = diabetes_X[:-20]
diabetes_X_test = diabetes_X[-20:]
# Разделите цели на обучающие/тестовые наборы
diabetes_y_train = diabetes_y[:-20]
diabetes_y_test = diabetes_y[-20:]
# Создание объекта линейной регрессии
regr = linear_model.LinearRegression()
# Обучите модель с помощью обучающих наборов
regr.fit(diabetes_X_train, diabetes_y_train)
# Делайте прогнозы, используя набор тестов
diabetes_y_pred = regr.predict(diabetes_X_test)
# Среднеквадратичная ошибка
print("Mean squared error: %.2f" % mean_squared_error(diabetes_y_test, diabetes_y_pred))
Вывод
Mean squared error: 2548.07
Логистическая регрессия — это алгоритм классификации. Это алгоритм принятия решений, что означает, что он ищет границы между двумя классами и моделирует вероятности одного класса. Поскольку ввод дискретный и может принимать два значения, он обычно используется для двоичной классификации.
Целевая переменная в линейной регрессии является непрерывной, что означает, что она может принимать любое действительное числовое значение, тогда как в логистической регрессии мы хотим, чтобы наши выходные данные были вероятностями (от 0 до 1). Логистическая регрессия является производной от линейной регрессии, но она добавляет дополнительный уровень сигмовидной функции, чтобы гарантировать, что выходные данные остаются между 0 и 1.
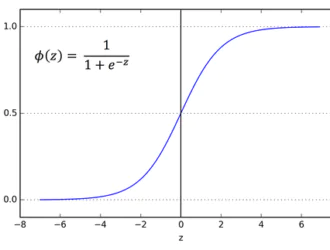
Логистическая регрессия — это простой и широко используемый алгоритм машинного обучения, особенно для задач двоичной классификации. Это расширение алгоритма линейной регрессии использует сигмовидную функцию активации для ограничения выходной переменной между 0 и 1. Предположим, нам нужно построить модель машинного обучения, тогда каждая точка данных независимой переменной будет x1 * w1 + x2 * w2… и так on, и это даст значение от 0 до 1 при передаче через функцию активации, если мы используем 0,50 в качестве решающего значения или порога. Тогда любой результат больше 0,5 считается равным 1, а любой результат меньше этого считается нулевым. Функция активации сигмовидной кишки представлена как:
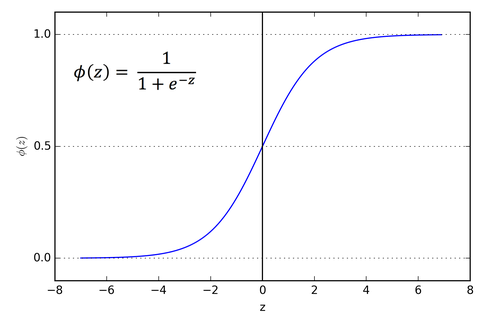
Из графика видно, что выходная переменная ограничена между 0 и 1.
В сценариях с более чем двумя классами мы используем подход классификации «один против всех». Разделение набора данных с несколькими классами на несколько задач двоичной классификации — вот что такое One vs. Rest.
По каждой задаче двоичной классификации обучается двоичный классификатор, и прогнозы делаются с использованием модели с максимальной достоверностью.
Ниже приведен сценарий из официальной документации scikit-learn для классификации цветка ириса на основе различных характеристик.
>>> from sklearn.datasets import load_iris >>> from sklearn.linear_model import LogisticRegression >>> X, y = load_iris(return_X_y=True) >>> clf = LogisticRegression(random_state=0).fit(X, y) >>> clf.predict(X[:2, :]) array( 01, 1.8...e (X, y) 0.97...
Мы познакомились с логистической и линейной регрессией, обсудили лежащую в основе математику и рассмотрели часть реализации каждой из них. Мы можем сделать вывод, что линейная регрессия помогает прогнозировать непрерывные переменные, в то время как логистическая регрессия используется в случае дискретных целевых переменных. Логистическая регрессия делает это, применяя сигмовидную функцию активации к уравнению линейной регрессии.
(1 оценок, среднее: 5,00 из 5)
Загрузка...
