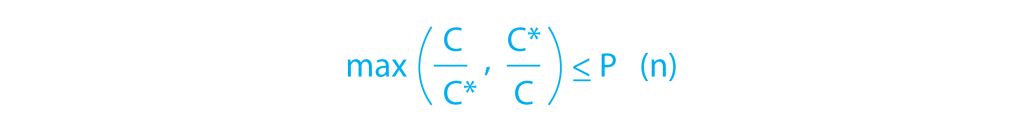Алгоритмы аппроксимации

Приближенный алгоритм – это метод приближения к NP-COMPLETENESS задачи оптимизации. Этот метод не обеспечивает наилучшего решения. Цель алгоритма аппроксимации – максимально приблизиться к оптимальному значению за разумный промежуток времени, который не превышает полиномиального времени. Алгоритмы аппроксимации и эвристические алгоритмы являются примерами таких алгоритмов.

Понимание Алгоритмов аппроксимации

Алгоритмы аппроксимации – это алгоритмы, предназначенные для нахождения почти оптимальных решений задач оптимизации эффективным с вычислительной точки зрения способом. Эти задачи обычно включают поиск наилучшего решения среди огромного количества возможностей, когда нахождение точного оптимального решения непрактично или требует непомерно длительного времени вычислений.

Коэффициенты производительности

Предположим, что мы работаем над задачей оптимизации, где каждое решение имеет свою стоимость. Приблизительный алгоритм возвращает юридическое решение, но стоимость этого юридического решения может быть неоптимальной.
Например, предположим, что мы рассматриваем вершинное покрытие минимального размера (VC). Приближенный алгоритм возвращает для нас VC, но размер (стоимость) может быть не минимизирован.

Другим примером может быть набор, не зависящий от максимального размера (IS). Приближенный алгоритм возвращает для нас IS, но размер (стоимость) может быть меньше оптимального. Пусть C – стоимость решения приближенного алгоритма, а C* – стоимость оптимального решения. Для входного размера n мы говорим, что приближенный алгоритм имеет приблизительное соотношение P (n), где

Коэффициент аппроксимации интуитивно измеряет, насколько сильно приблизительный ответ отличается от оптимального решения. Большой (малый) коэффициент аппроксимации указывает на то, что ответ значительно хуже (или примерно равен) идеального решения. Поскольку P (n) всегда равно единице, мы можем записать P, если отношение не зависит от n . В результате алгоритм с 1 приближением дает наилучшее решение. В некоторых выпусках используются методы аппроксимации за полиномиальное время со скромными постоянными приближенными соотношениями, в то время как в других есть хорошо известные алгоритмы аппроксимации за полиномиальное время с приближенными соотношениями, которые возрастают с увеличением n.

Ключевые особенности алгоритмов аппроксимации

1. Гарантии производительности: Алгоритмы аппроксимации предоставляют гарантии производительности, которые количественно определяют качество их решений. Эти гарантии выражаются в виде коэффициентов аппроксимации или границ, определяющих, насколько близко решение алгоритма к оптимальному решению.

2. Сложность за полиномиальное время: Алгоритмы аппроксимации фокусируются на предоставлении эффективных решений в рамках сложности за полиномиальное время. Они идут на компромисс между оптимальностью и эффективностью, что позволяет им решать крупномасштабные задачи, которые в противном случае были бы неразрешимыми.

3. Подходы, ориентированные на конкретную проблему: Различные алгоритмы аппроксимации используют методы и эвристику, ориентированные на конкретную проблему, основанные на характере задачи оптимизации. Эти методы используют специфические свойства задачи для эффективного поиска решений, близких к оптимальным.

Приложения алгоритмов аппроксимации

Алгоритмы аппроксимации находят применение в различных областях и доменах. Некоторые известные примеры включают:

1. Проектирование сети: Алгоритмы аппроксимации используются для решения таких задач, как минимальные связующие деревья, местоположение объекта и сетевое подключение. Эти алгоритмы обеспечивают эффективное планирование и оптимизацию сетевой инфраструктуры.

2. Планирование и балансировка нагрузки: Алгоритмы аппроксимации используются для планирования задач, распределения ресурсов и балансировки нагрузок в таких системах, как центры обработки данных и облачные вычисления. Они обеспечивают эффективное использование ресурсов при обеспечении приемлемого качества обслуживания.

3. Задача коммивояжера: Задача коммивояжера, классическая задача оптимизации, направлена на поиск кратчайшего возможного маршрута для посещения набора городов. Алгоритмы аппроксимации обеспечивают решения, которые находятся в пределах коэффициента оптимального решения, позволяя эффективно планировать маршруты и оптимизировать логистику.

4. Проблема упаковки ящиков: В ситуациях, когда товары разного размера необходимо упаковать в ограниченное количество ящиков, алгоритмы аппроксимации предлагают эффективные подходы для достижения почти оптимальных стратегий упаковки. Это находит применение в логистике, управлении запасами и распределении ресурсов.

Заключение

Алгоритмы аппроксимации устраняют разрыв между стремлением к оптимальным решениям и ограниченностью вычислительных ресурсов. Жертвуя оптимальностью в пользу эффективности, эти алгоритмы обеспечивают почти оптимальные решения за разумное время вычислений. Благодаря гарантиям производительности и методам решения конкретных задач алгоритмы аппроксимации находят применение в различных областях, обеспечивая эффективную оптимизацию в сложных сценариях. Поскольку границы вычислительной осуществимости продолжают расширяться, алгоритмы аппроксимации играют жизненно важную роль в решении задач оптимизации во многих областях.

Часто задаваемые вопросы (FAQs)

Вопрос 1. В чем основное различие между точными алгоритмами и алгоритмами аппроксимации?

Точные алгоритмы нацелены на нахождение оптимального решения проблемы, гарантирующего наилучший возможный результат. С другой стороны, алгоритмы аппроксимации сосредоточены на предоставлении почти оптимальных решений за полиномиальное время, что позволяет эффективно решать сложные задачи.

Вопрос 2. Как алгоритмы аппроксимации гарантируют качество своих решений?

Алгоритмы аппроксимации предоставляют гарантии производительности в виде коэффициентов аппроксимации или границ. Эти гарантии определяют, насколько близко решение алгоритма к оптимальному решению. Например, алгоритм аппроксимации может гарантировать решение с точностью до 2 от оптимального решения.

Вопрос 3. Всегда ли алгоритмы аппроксимации эффективны с точки зрения временной сложности?

Да, одной из ключевых характеристик алгоритмов аппроксимации является их способность выдавать решения за полиномиальное время сложности. Такая эффективность позволяет им решать крупномасштабные задачи, которые были бы неразрешимы для точных алгоритмов, хотя эффективность может быть достигнута ценой отказа от оптимальности.

Вопрос 4. Могут ли алгоритмы аппроксимации обеспечивать решения, сколь угодно близкие к оптимальному решению?

Нет, алгоритмы аппроксимации обычно предоставляют решения, которые находятся в пределах определенного коэффициента или границы оптимального решения. Конкретный коэффициент аппроксимации зависит от задачи и используемого алгоритма. Хотя решения не всегда являются оптимальными, они все же считаются приемлемыми и полезными на практике.

Вопрос 5. Существуют ли какие-либо задачи оптимизации, в которых алгоритмы аппроксимации последовательно обеспечивают оптимальные решения?

В общем случае алгоритмы аппроксимации не гарантируют оптимальных решений. Однако существуют некоторые особые случаи, когда алгоритм аппроксимации может обеспечить точное оптимальное решение. Эти случаи обычно возникают, когда задача имеет определенную структуру или удовлетворяет определенным условиям, которые обеспечивают оптимальную аппроксимацию.

(Пока оценок нет)

Загрузка...