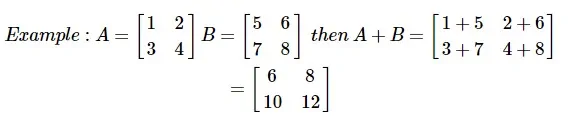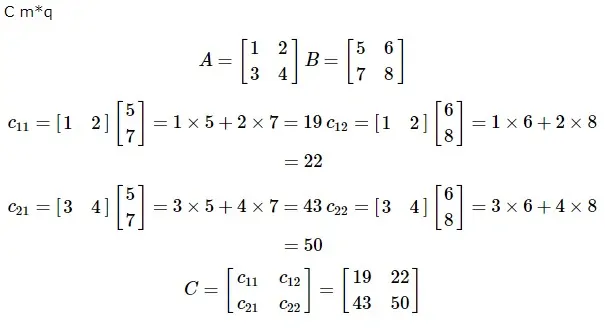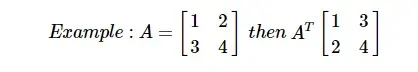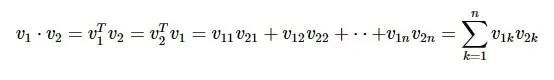TensorFlow — Математические основы

Важно понять математические понятия, необходимые для TensorFlow, прежде чем создавать базовое приложение в TensorFlow. Математика считается сердцем любого алгоритма машинного обучения. Именно с помощью основных понятий математики определяется решение для конкретного алгоритма машинного обучения.
Вектор
Массив чисел, который является либо непрерывным, либо дискретным, определяется как вектор. Алгоритмы машинного обучения работают с векторами фиксированной длины для лучшего генерирования выходных данных.
Алгоритмы машинного обучения работают с многомерными данными, поэтому векторы играют решающую роль.
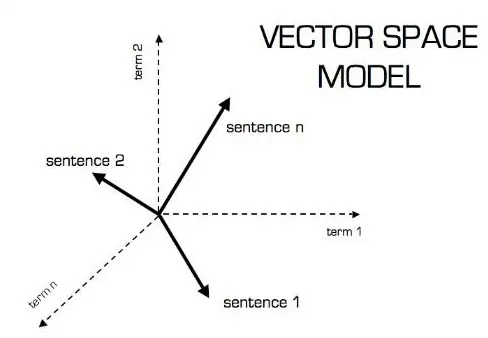
Графическое представление векторной модели показано ниже:
Скаляр
Скаляр может быть определен как одномерный вектор. Скаляры — это те, которые включают только величину и отсутствие направления. Со скалярами нас интересует только величина.
Примеры скаляров включают в себя параметры веса и роста детей.
Матрица
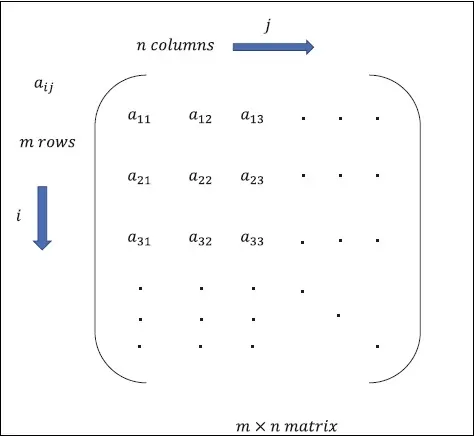
Матрица может быть определена как многомерные массивы, которые расположены в формате строк и столбцов. Размер матрицы определяется длиной строки и длиной столбца. На следующем рисунке показано представление любой указанной матрицы.
Рассмотрим матрицу с «m» строками и «n» столбцами, как упомянуто выше, представление матрицы будет определено как «m * n matrix», которое также определило длину матрицы.
Математические вычисления
В этом разделе мы узнаем о различных математических вычислениях в TensorFlow.
Добавление матриц
Добавление двух или более матриц возможно, если матрицы имеют одинаковое измерение. Добавление подразумевает добавление каждого элемента в соответствии с заданной позицией.
Рассмотрим следующий пример, чтобы понять, как работает сложение матриц:
Вычитание матриц
Вычитание матриц работает аналогично добавлению двух матриц. Пользователь может вычесть две матрицы при условии, что размеры равны.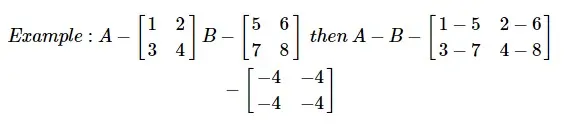
Умножение матриц
Для того чтобы две матрицы A m * n и B p * q были умножаемыми, n должно быть равно p. Полученная матрица:
Транспонирование матрицы
Транспонирование матрицы A, m * n обычно представляется AT (транспонирование) n * m и получается путем транспонирования векторов столбцов в качестве векторов строк.
Точечное произведение векторов
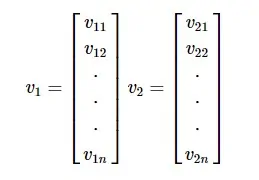
Любой вектор размерности n можно представить в виде матрицы v = R ^ n * 1.
Точечное произведение двух векторов является суммой произведений соответствующих компонентов — Компонентов вдоль одного измерения и может быть выражено как
Пример точечного произведения векторов приведен ниже: