Монотонные отношения

Различные отношения между несколькими переменными могут помочь нам получить дополнительное представление о наших данных в математике. В целом отношения могут быть растущими, линейными или убывающими. Различные тесты также применяются для измерения этих отношений между переменными. Мы рассмотрим монотонную связь между двумя переменными и способы ее проверки.

Что такое ковариация?

Ковариация — это статистика, которая исследует, как две случайные величины изменяются вместе, и измеряет их взаимосвязь. Разница между дисперсией и ковариацией заключается в том, что дисперсия измеряет вариацию одной переменной, тогда как ковариация измеряет вариацию двух переменных по отношению друг к другу. Мы также можем сказать, что дисперсия показывает ковариацию переменной самой с собой. Направление связи между двумя переменными определяется ковариацией в пределах от (-) бесконечности до (+) бесконечности.

Что такое корреляция?

Корреляция — это масштабированная мера ковариации, используемая для определения возможности связи между двумя переменными. Коэффициент корреляции представляет собой одномерную статистику в диапазоне от (-1) до (+1). (-1) указывает на сильную отрицательную связь между двумя переменными, тогда как (+1) указывает на сильную положительную связь.

Что такое монотонная связь?

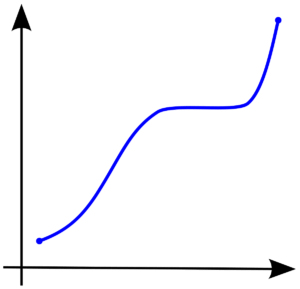
В случае, если одна переменная увеличивается в тандеме с другой или значение одной переменной увеличивается, значение другой переменной уменьшается; существует монотонная связь между двумя переменными. Скорость, с которой происходит повышение или снижение, не обязательно должна быть одинаковой для обеих переменных. Монотонная зависимость может быть линейной зависимостью, в которой обе переменные увеличиваются или уменьшаются с одинаковой скоростью. На приведенном ниже графике показано, как одна переменная увеличивается с другой. Это называется положительным монотонным отношением.

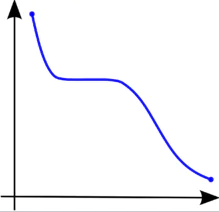
На приведенном ниже графике показана отрицательная монотонная корреляция, когда одна переменная уменьшается с другой.

Строго монотонный и нестрого монотонный

Если дельта одной переменной всегда связана с дельтой в том же направлении по другой переменной, то связь называется строго монотонной. Например, когда одна переменная растет, другая растет вместе с ней, а другая падает, когда падает одна переменная. С другой стороны, в простой монотонной связи две переменные в какой-то момент могут быть одинаковыми.

Количественная оценка монотонных отношений с использованием коэффициента ранговой корреляции Спирмена

Коэффициент ранговой корреляции Спирмена показывает, как связаны между собой две переменные. По сути, он обеспечивает меру монотонности связи между двумя переменными, т. е. эффективно монотонная функция может конкретизировать связь между двумя переменными. Константа Спирмена имеет диапазон от -1 до +1 включительно. Абсолютно монотонные функции могут выражать связь между двумя переменными, если значение равно +1 или -1. Чтобы вычислить значение коэффициента Спирмена, сначала преобразуйте необработанные данные в ранжированные данные для обеих переменных X и Y, а затем используйте следующую формулу для ранжированных переменных.

Вывод

В этой статье мы рассмотрели несколько терминов, связанных с монотонными отношениями. Ковариация измеряет, насколько тесно связаны две или более переменных, и ее значение может быть любым действительным числом. Другой способ измерения отношений — использование корреляции. Когда одна переменная увеличивается или уменьшается в ответ на увеличение другой переменной, это называется монотонной зависимостью. Монотонная связь между переменными измеряется с помощью широко используемого коэффициента ранговой корреляции Спирмена.

(Пока оценок нет)

Загрузка...