ИТ Блог. Администрирование серверов на основе Linux (Ubuntu, Debian, CentOS, openSUSE)
(1 оценок, среднее: 5,00 из 5)
Загрузка...
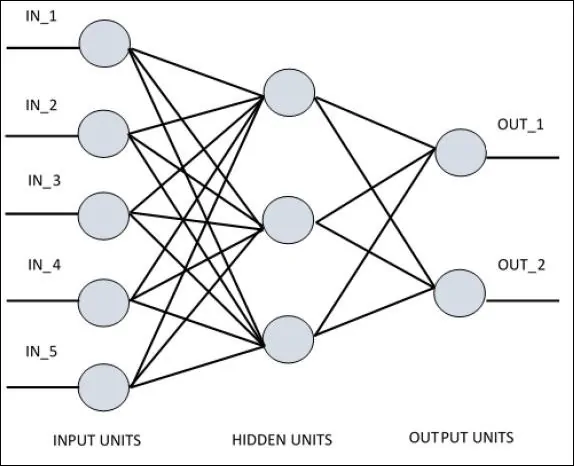
Для понимания однослойного персептрона важно понимать Искусственные Нейронные Сети (ANN). Искусственные нейронные сети — это система обработки информации, механизм которой вдохновлен функциональностью биологических нейронных цепей. Искусственная нейронная сеть обладает множеством процессорных блоков, связанных друг с другом. Ниже приводится схематическое изображение искусственной нейронной сети:
Диаграмма показывает, что скрытые блоки связываются с внешним слоем. При этом блоки ввода и вывода обмениваются данными только через скрытый слой сети.
Схема связи с узлами, общее количество слоев и уровень узлов между входами и выходами с количеством нейронов на слой определяют архитектуру нейронной сети.
Есть два типа архитектуры. Эти типы ориентированы на функциональность искусственных нейронных сетей следующим образом:
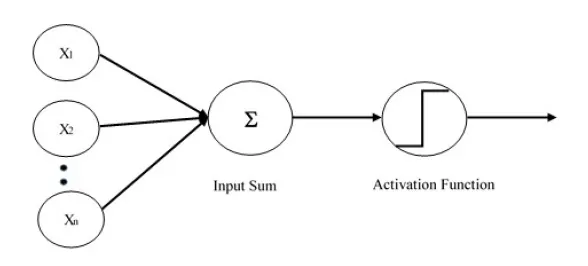
Однослойный персептрон — первая предложенная нейронная модель. Содержимое локальной памяти нейрона состоит из вектора весов. Вычисление однослойного персептрона выполняется по вычислению суммы входного вектора, каждое со значением, умноженным на соответствующий элемент вектора весов. Значение, которое отображается на выходе, будет входом функции активации.
Давайте сосредоточимся на реализации однослойного персептрона для задачи классификации изображений с использованием TensorFlow. Наилучшим примером для иллюстрации однослойного персептрона является представление «логистической регрессии».
Теперь рассмотрим следующие основные этапы обучения логистической регрессии:
Полный код для оценки логистической регрессии упомянут ниже:
# Импорт MINST data
from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets("/tmp/data/", one_hot = True)
import tensorflow as tf
import matplotlib.pyplot as plt
# Параметры
learning_rate = 0.01
training_epochs = 25
batch_size = 100
display_step = 1
# входной сигнал диаграммы tf
x = tf.placeholder("float", [None, 784]) # изображение данных по mnist формы 28*28 = 784
y = tf.placeholder("float", [None, 10]) # 0-9 распознавание цифр = > 10 классов
# Создание модели
# Установка весов модели
W = tf.Variable(tf.zeros([784, 10]))
b = tf.Variable(tf.zeros([10]))
# Построить модель
activation = tf.nn.softmax(tf.matmul(x, W) + b) # Softmax
# Минимизировать ошибку, используя перекрестную энтропию
cross_entropy = y*tf.log(activation)
cost = tf.reduce_mean\ (-tf.reduce_sum\ (cross_entropy,reduction_indices = 1))
optimizer = tf.train.\ GradientDescentOptimizer(learning_rate).minimize(cost)
# Настройки участка
avg_set = []
epoch_set = []
# Инициализация переменных init = tf.initialize_all_variables()
# Запуск на графике
with tf.Session() as sess:
sess.run(init)
# Тренировочный цикл
for epoch in range(training_epochs):
avg_cost = 0.
total_batch = int(mnist.train.num_examples/batch_size)
# Цикл по всем партиям
for i in range(total_batch):
batch_xs, batch_ys = \ mnist.train.next_batch(batch_size)
# Обучение подгонке с использованием пакетных данных
sess.run(optimizer, \ feed_dict = {x: batch_xs, y: batch_ys})
# Вычислить средние потери
avg_cost += sess.run(cost, \ feed_dict = {x: batch_xs, \ y: batch_ys})/total_batch
# Отображение журналов на шаг epoch
if epoch % display_step == 0:
print ("Epoch:", '%04d' % (epoch+1), "cost=", "{:.9f}".format(avg_cost))
avg_set.append(avg_cost) epoch_set.append(epoch+1)
print ("Фаза обучения завершена")
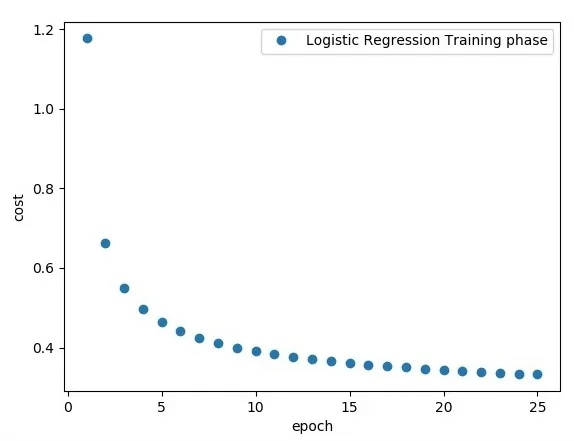
plt.plot(epoch_set,avg_set, 'o', label = 'Этап обучения логистической регрессии')
plt.ylabel('cost')
plt.xlabel('epoch')
plt.legend()
plt.show()
# Тест модели
correct_prediction = tf.equal(tf.argmax(activation, 1), tf.argmax(y, 1))
# Расчет точности
accuracy = tf.reduce_mean(tf.cast(correct_prediction, "float")) print
("Точность модели:", accuracy.eval({x: mnist.test.images, y: mnist.test.labels}))
Логистическая регрессия рассматривается как прогнозный анализ. Логистическая регрессия используется для описания данных и объяснения взаимосвязи между одной зависимой двоичной переменной и одной или несколькими номинальными или независимыми переменными.
