Алгоритм невосстанавливающего деления для целого числа без знака

В мире компьютерной арифметики деление является фундаментальной операцией, которая играет решающую роль в различных приложениях, начиная от числовых вычислений и заканчивая цифровой обработкой сигналов. Среди различных алгоритмов деления Алгоритм невосстанавливающего деления для целых чисел без знака выделяется как эффективный и интригующий метод. Этот алгоритм используется для выполнения деления без необходимости восстановления промежуточных остатков, предлагая упрощенный подход к достижению точных частных результатов. В этой статье мы углубляемся в механику невосстанавливающего алгоритма деления, исследуя его принципы, преимущества и пошаговое выполнение. Разбираясь в этом алгоритме, мы получаем представление о внутренней работе современных цифровых систем и получаем более глубокое представление об алгоритмах, которые питают наш вычислительный мир.
Что такое алгоритм невосстанавливающего деления для целого числа без знака?
Алгоритм невосстанавливающего деления — это метод, используемый для выполнения операций деления над целыми числами без знака, не полагаясь на восстановление промежуточных остатков. Это итерационный подход, который аппроксимирует частное и обновляет остаток на каждой итерации, что приводит к точному результату деления.
Вот обзор того, как работает алгоритм невосстанавливающего деления:
Инициализация:
Загрузите делимое и делитель в отдельные регистры.
Инициализируйте счетчик для отслеживания количества итераций.
Сравнение и корректировка:
- Сравните делитель с накопленным остатком.
- Если остаток больше или равен делителю, вычтите делитель из остатка и установите флаг «заимствовать» равным 0.
- Если остаток меньше делителя, установите флаг заимствования равным 1.
Сдвиг:
Сдвиньте накопленный остаток влево на одну позицию.
Обновить флаг заимствования:
Если флаг заимствования равен 1, добавьте делитель к остатку.
Итерация:
Повторяйте шаги 2-4 в течение фиксированного числа итераций (обычно равного количеству битов в операндах) или до тех пор, пока счетчик не достигнет желаемого значения.
Формирование частного:
Частное формируется из значения счетчика.
Окончательная корректировка:
После итераций, если остаток больше или равен делителю, вычтите делитель из остатка, чтобы получить окончательный остаток.
Результат:
Частное и остаток, полученные с помощью алгоритма, представляют собой результат операции деления.
Алгоритм невосстанавливающего деления позволяет избежать необходимости восстановления промежуточных остатков путем корректировки остатка непосредственно на основе сравнений и заимствованных флагов. Он особенно полезен в аппаратных реализациях, где параллельная обработка возможна благодаря фиксированному числу итераций.
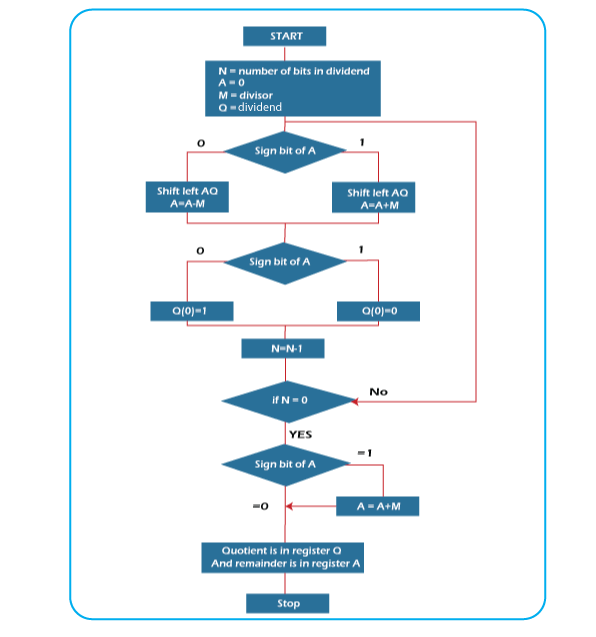
Давайте обсудим блок-схему алгоритма невосстанавливающего деления для целого числа без знака.
Блок-схема для алгоритма невосстанавливающего деления для целого числа без знака
Теперь давайте углубимся в последовательные этапы алгоритма невосстанавливающего деления, которые описаны ниже:
Шаг 1: Инициализация включает загрузку соответствующих значений в регистры. В частности, регистр A инициализируется значением 0, регистр M содержит делитель, регистр Q сохраняет делимое, а N обозначает количество битов в делимом.
Шаг 2: Переходя к следующему этапу, мы оцениваем знаковый бит регистра A.
Шаг 3: Если этот бит в регистре A равен 1, мы сдвигаем значение AQ влево и выполняем A = A + M. Напротив, если бит равен 0, мы снова сдвигаем значение AQ влево, но выполняем A = A – M. В последнем случае дополнение M к 2 добавляется к регистру A, и результат заменяет A.
Шаг 4: Выполняется последующая проверка знакового бита A.
Шаг 5: Когда знаковый бит в регистре A равен 1, Q[0] устанавливается равным 0. И наоборот, если бит равен 0, Q[0] устанавливается равным 1. Здесь Q[0] обозначает младший значащий бит Q.
Шаг 6: После этого N уменьшается, действуя в процессе как счетчик.
Шаг 7: Если N равно 0, прогрессия переходит к следующему шагу. В противном случае требуется возврат к шагу 2.
Шаг 8: Если знаковый бит регистра A равен 1, мы переходим к A = A + M.
Шаг 9: Завершая алгоритм, на этом последнем шаге регистр A содержит остаток, в то время как регистр Q содержит частное.
Давайте посмотрим пример, который объяснит процесс алгоритма невосстанавливающего деления для целого числа без знака.
Пример алгоритма невосстанавливающего деления для целого числа без знака
В этом примере мы выполним невосстанавливающий алгоритм деления с помощью целого числа без знака.
| N | M | A | Q | Действие |
|---|---|---|---|---|
| 4 | 00011 | 00000 | 1011 | Начать |
| 00011 | 00001 | 011_ | Сдвиг влево AQ | |
| 00011 | 11110 | 011_ | A = A – M | |
| 3 | 00011 | 11110 | 0110 | Q[0] = 0 |
| 00011 | 11100 | 110_ | Сдвиг влево AQ | |
| 00011 | 11111 | 110_ | A = A + M | |
| 2 | 00011 | 11111 | 1100 | Q[0] = 0 |
| 00011 | 11111 | 100_ | Сдвиг влево AQ | |
| 00011 | 00010 | 100_ | A = A + M | |
| 1 | 00011 | 00010 | 1001 | Q[0] = 1 |
| 00011 | 00101 | 001_ | Сдвиг влево AQ | |
| 00011 | 00010 | 001_ | A = A – M | |
| 0 | 00011 | 00010 | 0011 | Q[0] = 1 |
Следовательно, регистр A содержит оставшееся значение 2, в то время как регистр Q содержит частное 3.
Заключение
Алгоритм невосстанавливающего деления демонстрирует элегантность алгоритмического оформления в компьютерной арифметике. Его способность эффективно выполнять операции деления с предсказуемой задержкой и потенциалом параллелизма делает его ценным инструментом в современных цифровых системах. Понимание механики этого алгоритма не только проливает свет на методы деления, но и дает представление об оптимизации аппаратных и программных реализаций. Поскольку мы продолжаем расширять границы вычислительной эффективности, алгоритмы, подобные алгоритму невосстанавливающего деления, остаются важными для достижения высокопроизводительных вычислений в различных областях.
ЧАСТО задаваемые вопросы по алгоритму невосстанавливающего деления для целого числа без знака
Вопрос 1: Что такое алгоритм невосстанавливающего деления?
Алгоритм невосстанавливающего деления — это метод, используемый для выполнения операций деления над целыми числами без знака, не полагаясь на традиционный процесс восстановления промежуточных остатков. Вместо этого этот алгоритм включает в себя серию шагов, которые итеративно аппроксимируют частное и корректируют остаток, что приводит к точному результату деления.
Вопрос 2: Как работает алгоритм невосстанавливающего деления?
Алгоритм включает в себя следующие основные этапы:
- Инициализация: Загрузка делимого и делителя в отдельные регистры.
- Сравнение: сравните делитель с накопленным остатком.
- Сдвиг и корректировка: сдвиньте накопленный остаток и обновите его на основе результата сравнения.
- Итерация: повторяйте процесс сравнения и корректировки до тех пор, пока не будет достигнуто определенное количество итераций.
- Формирование частного: Частное формируется из числа итераций и окончательной корректировки.
Вопрос 3: Каковы преимущества алгоритма невосстанавливающего деления?
Алгоритм невосстанавливающего деления обладает рядом преимуществ, в том числе:
- Более быстрое выполнение: По сравнению с алгоритмами восстановления, невосстанавливающие алгоритмы часто требуют меньшего количества итераций, что приводит к более быстрым операциям деления.
- Параллелизм: алгоритм допускает параллельное выполнение, что делает его пригодным для аппаратной реализации.
- Предсказуемая задержка: количество итераций фиксировано, что приводит к предсказуемой задержке, что крайне важно для приложений реального времени.
Q4: Есть ли какие-либо недостатки или ограничения у этого алгоритма?
Хотя алгоритм невосстанавливающего деления имеет свои преимущества, он также имеет некоторые ограничения, такие как:
- Сложность: Алгоритм требует дополнительных шагов для управления невосстанавливающим подходом, что потенциально приводит к более сложной схеме или коду.
- Начальный сдвиг делителя: Начальный сдвиг делителя может привести к задержке до того, как алгоритм начнет процесс деления.
Редактор: AndreyEx