Структуры данных и алгоритмы
Структуры данных и алгоритмы — это две фундаментальные области информатики, которые изучают способы хранения и обработки данных. Структуры данных обеспечивают эффективный способ хранения данных, а алгоритмы обеспечивают эффективный способ обработки данных.
Структуры данных
Структуры данных — это способы организации данных для эффективного хранения и доступа к ним. Они могут быть простыми, такими как массивы, или сложными, такими как деревья или графы.
Основные типы структур данных:
- Массивы — это линейные структуры данных, в которых данные хранятся в последовательных ячейках памяти. Массивы просты в использовании, но они могут быть неэффективными для хранения данных, которые не являются последовательными.
- Связные списки — это линейные структуры данных, в которых данные хранятся в связанных ячейках памяти. Связи указывают на следующую ячейку в списке. Священные списки более гибкие, чем массивы, но они могут быть менее эффективными для доступа к данным в середине списка.
- Дерева — это иерархические структуры данных, в которых данные хранятся в виде дерева. Каждое дерево имеет корень, который является родительским элементом для других элементов дерева. Деревья могут быть эффективными для хранения данных, которые имеют иерархическую структуру.
- Графы — это неориентированные структуры данных, в которых данные хранятся в виде сети. Графы могут быть эффективными для хранения данных, которые имеют отношения между собой.
Алгоритмы
Алгоритмы — это последовательности действий, которые выполняются для решения задачи. Они могут быть простыми, такими как поиск элемента в массиве, или сложными, такими как сортировка массива.
Основные типы алгоритмов:
- Поиск — это алгоритм для нахождения элемента в наборе данных. Существуют различные типы алгоритмов поиска, такие как линейный поиск, бинарный поиск и поиск по хэш-таблице.
- Сортировка — это алгоритм для упорядочивания набора данных. Существуют различные типы алгоритмов сортировки, такие как сортировка пузырьком, сортировка выбором, сортировка вставкой, сортировка быстрая и сортировка пирамидальная.
- Объединение — это алгоритм для объединения двух отсортированных наборов данных в один отсортированный набор.
- Деление — это алгоритм для разделения отсортированного набора данных на два отсортированных набора.
- Рекурсия — это метод решения задачи путем многократного вызова самого себя.
Взаимосвязь между структурами данных и алгоритмами
Структуры данных и алгоритмы тесно связаны друг с другом. Выбор структуры данных для хранения данных зависит от типа данных и операций, которые будут выполняться над данными. Выбор алгоритма для выполнения задачи зависит от типа задачи и характеристик данных.
Значение структур данных и алгоритмов
Структуры данных и алгоритмы являются фундаментальными концепциями информатики. Они используются в различных областях, включая разработку программного обеспечения, машинное обучение, обработку естественного языка и компьютерную графику.
Примеры использования структур данных и алгоритмов:
- Разработка программного обеспечения: Структуры данных и алгоритмы используются для разработки различных программных приложений, таких как операционные системы, базы данных и веб-сайты.
- Машинное обучение: Структуры данных и алгоритмы используются для разработки алгоритмов машинного обучения, таких как классификация, регрессия и кластеризация.
- Обработка естественного языка: Структуры данных и алгоритмы используются для разработки алгоритмов обработки естественного языка, таких как распознавание речи, перевод и поиск.
- Компьютерная графика: Структуры данных и алгоритмы используются для разработки алгоритмов компьютерной графики, таких как рендеринг, трассировка лучей и анимация.
Изучение структур данных и алгоритмов
Изучение структур данных и алгоритмов является важным для любого, кто хочет стать успешным программистом. Эти концепции являются фундаментальными для разработки эффективного и производительного программного обеспечения.
Существует множество ресурсов, которые могут помочь вам изучить структуры данных и алгоритмы. Вы можете найти онлайн-курсы, книги и статьи, которые охватывают эти темы. Вы также можете найти сообщества и форумы, где вы можете задать вопросы и получить помощь от других программистов.
Оценка сложности алгоритмов
Оценка сложности алгоритмов — это процесс определения того, как время и память, необходимые для выполнения алгоритма, зависят от размера входных данных.
Существует два основных типа сложности алгоритмов:
- Временная сложность — это количество времени, необходимого для выполнения алгоритма.
- Пространственная сложность — это количество памяти, необходимой для выполнения алгоритма.
Временную сложность алгоритмов можно оценивать различными способами. Один из способов — это использовать асимптотическую оценку. Асимптотическая оценка — это оценка, которая описывает поведение алгоритма для больших значений входных данных.
Существует несколько типов асимптотических оценок. Наиболее распространенными являются:
- Оценка O(n) — это оценка, которая говорит, что время выполнения алгоритма увеличивается пропорционально количеству входных данных.
- Оценка O(n^2) — это оценка, которая говорит, что время выполнения алгоритма увеличивается пропорционально квадрату количества входных данных.
- Оценка O(n^3) — это оценка, которая говорит, что время выполнения алгоритма увеличивается пропорционально кубу количества входных данных.
Пространственная сложность алгоритмов также можно оценивать различными способами. Один из способов — это использовать асимптотическую оценку.
Существует несколько типов асимптотических оценок пространства. Наиболее распространенными являются:
- Оценка O(n) — это оценка, которая говорит, что объем памяти, необходимый для выполнения алгоритма, увеличивается пропорционально количеству входных данных.
- Оценка O(n^2) — это оценка, которая говорит, что объем памяти, необходимый для выполнения алгоритма, увеличивается пропорционально квадрату количества входных данных.
- Оценка O(n^3) — это оценка, которая говорит, что объем памяти, необходимый для выполнения алгоритма, увеличивается пропорционально кубу количества входных данных.
Выбор структуры данных и алгоритма
При выборе структуры данных и алгоритма для решения задачи необходимо учитывать следующие факторы:
- Тип данных — необходимо выбрать структуру данных, которая поддерживает тип данных, с которым необходимо работать.
- Операции — необходимо выбрать структуру данных, которая поддерживает операции, которые необходимо выполнять над данными.
- Характеристики данных — необходимо учитывать характеристики данных, такие как размер, структура и частота использования.
- Сложность — необходимо выбрать структуру данных и алгоритм с наименьшей сложностью, соответствующей потребностям задачи.
Примеры выбора структуры данных и алгоритма
- Для хранения списка чисел можно использовать массив или связанный список. Массив — это более простой вариант, но он может быть менее эффективным для доступа к данным в середине списка. Связанный список более гибкий, но он требует больше памяти.
- Для сортировки списка чисел можно использовать сортировку пузырьком, сортировку выбором или быструю сортировку. Сортировка пузырьком — это самый простой вариант, но она наименее эффективна. Сортировка выбором более эффективна, чем сортировка пузырьком, но она все еще не очень эффективна. Быстрая сортировка — это наиболее эффективный вариант.
Заключение
Структуры данных и алгоритмы являются фундаментальными концепциями информатики. Они используются в различных областях, включая разработку программного обеспечения, машинное обучение, обработку естественного языка и компьютерную графику. Изучение структур данных и алгоритмов является важным для любого, кто хочет стать успешным программистом.
Алгоритм обратного отслеживания с примером
Что такое карта структуры данных

Лучший первый поиск в области искусственного интеллекта

Алгоритмы аппроксимации

Что такое временной ряд

Монотонные отношения
Алгоритм топологической сортировки
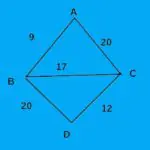
Алгоритм Крускала
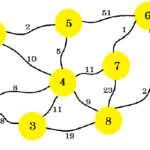
Алгоритм Прима