TensorFlow — Формирование графиков

Дифференциальное уравнение в частных производных (PDE) — это дифференциальное уравнение, которое включает в себя частные производные с неизвестной функцией нескольких независимых переменных. Что касается дифференциальных уравнений в частных производных, мы сосредоточимся на создании новых графиков.
Предположим, есть пруд размером 500 * 500 кв.
N = 500
Теперь мы вычислим уравнение в частных производных и сформируем соответствующий граф, используя его. Рассмотрим шаги, приведенные ниже для вычисления графа.
Шаг 1 — Импорт библиотек для симуляции.
import tensorflow as tf import numpy as np import matplotlib.pyplot as plt
Шаг 2 — Включите функции для преобразования двумерного массива в ядро свертки и упрощенную операцию свертки 2D.
def make_kernel(a): a = np.asarray(a) a = a.reshape(list(a.shape) + [1,1]) return tf.constant(a, dtype=1) def simple_conv(x, k): """Упрощенная 2D операция свертки""" x = tf.expand_dims(tf.expand_dims(x, 0), -1) y = tf.nn.depthwise_conv2d(x, k, [1, 1, 1, 1], padding = 'SAME') return y[0, :, :, 0] def laplace(x): """Вычислить 2D лапласиан массива""" laplace_k = make_kernel([[0.5, 1.0, 0.5], [1.0, -6., 1.0], [0.5, 1.0, 0.5]]) return simple_conv(x, laplace_k) sess = tf.InteractiveSession()
Шаг 3 — Включите количество итераций и вычислите график для отображения записей соответственно.
N = 500
# Начальные условия - некоторые капли дождя попали в пруд
# Set everything to zero
u_init = np.zeros([N, N], dtype = np.float32)
ut_init = np.zeros([N, N], dtype = np.float32)
# Некоторые капли дождя попали в пруд в случайных точках
for n in range(100):
a,b = np.random.randint(0, N, 2)
u_init[a,b] = np.random.uniform()
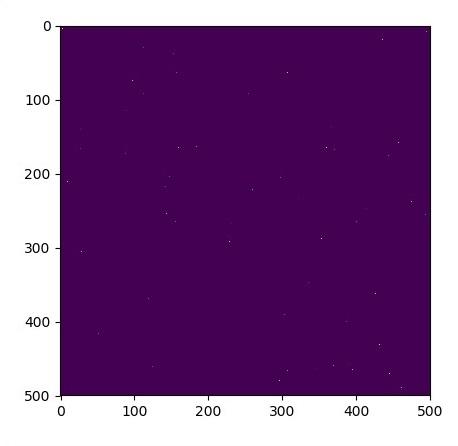
plt.imshow(u_init)
plt.show()
# Параметры:
# eps -- разрешение по времени
# damping -- демпфирование волны
eps = tf.placeholder(tf.float32, shape = ())
damping = tf.placeholder(tf.float32, shape = ())
# Создание переменных для состояния моделирования
U = tf.Variable(u_init)
Ut = tf.Variable(ut_init)
# Дискретизированные правила обновления PDE
U_ = U + eps * Ut
Ut_ = Ut + eps * (laplace(U) - damping * Ut)
# Операция по обновлению состояния
step = tf.group(U.assign(U_), Ut.assign(Ut_))
# Инициализировать состояние до начальных условий
tf.initialize_all_variables().run()
# Выполните 1000 шагов PDE
for i in range(1000):
# Step simulation
step.run({eps: 0.03, damping: 0.04})
# Визуализируйте каждые 50 шагов
if i % 500 == 0:
plt.imshow(U.eval())
plt.show()
Графики построены, как показано ниже: