Руководство по структуре данных кучи
Данные — это набор значений. Данные можно собирать и помещать в строку, в столбец, в таблицу или в виде дерева. Структура данных — это не только размещение данных в любой из этих форм. В вычислениях структура данных представляет собой любой из этих форматов, плюс взаимосвязь между значениями, плюс операции (функции), выполняемые над значениями. У вас уже должны быть базовые знания о древовидной структуре данных, прежде чем вы сюда приедете, поскольку содержащиеся в нем концепции будут использоваться здесь с небольшими пояснениями или без них. После этого продолжайте читать это руководство. Структура данных кучи — это полное или почти полное двоичное дерево, в котором дочерний элемент каждого узла равен или меньше по значению, чем значение его родительского элемента. В качестве альтернативы, это такое дерево, в котором значение родителя равно или меньше значения любого из его дочерних элементов. Значение (datum) дерева также называется ключом.
Иллюстрация структур данных кучи
Есть два типа кучи: максимальная и минимальная куча. Структура максимальной кучи — это когда максимальное значение является корнем, а значения становятся меньше по мере спуска дерева; любой родитель равен или больше по значению, чем любой из его непосредственных потомков. В структуре min-heap минимальным значением является корень, а значения становятся больше по мере спуска дерева; любой родитель равен или меньше по значению, чем любой из его непосредственных потомков. На следующих диаграммах первая — это максимальная куча, а вторая — минимальная куча:
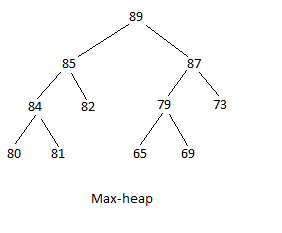 | 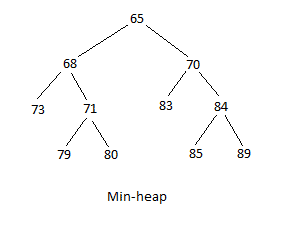 |
Для обеих куч обратите внимание, что для пары дочерних элементов не имеет значения, является ли тот, который слева, большее значение. Строка на уровне в дереве не обязательно должна заполняться от минимума до максимума слева; он также не обязательно заполняется от максимума до минимума слева.
Представление кучи в массиве
Чтобы программное обеспечение могло легко использовать кучу, куча должна быть представлена в виде массива. Максимальная куча выше, представленная в виде массива:
89, 85, 87, 84, 82, 79, 73, 80, 81, , , 65, 69prediv>
Это делается, начиная с корневого значения в качестве первого значения для массива. Значения размещаются непрерывно путем чтения дерева слева направо, сверху вниз. Если элемент отсутствует, его позиция в массиве пропускается. У каждого узла есть двое потомков. Если узел находится в индексе (позиции) n, его первый дочерний элемент в массиве имеет индекс 2n + 1, а его следующий дочерний элемент имеет индекс 2n + 2. 89 имеет индекс 0; его первый дочерний элемент, 85, имеет индекс 2 (0) + 1 = 1, а его второй дочерний элемент имеет индекс 2 (0) + 2 = 2. 85 находится под индексом 1; его первый дочерний элемент, 84, имеет индекс 2 (1) + 1 = 3, а его второй дочерний элемент, 82, имеет индекс 2 (1) + 2 = 4. 79 находится под индексом 5; его первый дочерний элемент, 65, имеет индекс 2 (5) + 1 = 11, а его второй дочерний элемент имеет индекс 2 (5) + 2 = 12. Формулы применяются к остальным элементам массива. Такой массив, в котором значение элемента и взаимосвязь между элементами подразумевается положением элемента, называется неявной структурой данных. Неявная структура данных для указанной выше минимальной кучи:
65, 68, 70, 73, 71, 83, 84, , , 79, 80, , , 85, 89
Вышеупомянутая максимальная куча — это полное двоичное дерево, но не полное двоичное дерево. Поэтому некоторые локации (позиции) в массиве пусты. Для полного двоичного дерева в массиве не будет пустых мест.
Теперь, если бы куча была почти полным деревом, например, если бы отсутствовало значение 82, тогда массив был бы:
89, 85, 87, 84, , 79, 73, 80, 81, , , 65, 69
В этой ситуации три ячейки пусты. Однако формулы все еще применимы.
Операции
Структура данных — это формат данных (например, дерево), плюс взаимосвязь между значениями, плюс операции (функции), выполняемые над значениями. Для кучи отношение, которое проходит через всю кучу, заключается в том, что родительский элемент должен быть равен или больше по значению, чем дочерние элементы, для максимальной кучи; а родительский элемент должен быть равен или меньше по значению, чем дочерние элементы, для минимальной кучи. Это отношение называется свойством кучи. Операции с кучей сгруппированы под заголовками «Создание», «Основные», «Внутренние» и «Проверка». Ниже приводится краткое описание операций с кучей:
Сводка операций с кучей
Есть определенные программные операции, которые являются общими для кучи, а именно:
Создание кучи
create_heap: создание кучи означает формирование объекта, представляющего кучу. В языке C вы можете создать кучу с типом объекта struct. Одним из членов структуры будет массив кучи. Остальные члены будут функциями (операциями) для кучи. Create_heap означает создание пустой кучи.
- Heapify: массив кучи — это частично отсортированный (упорядоченный) массив. Heapify означает предоставление массива кучи из несортированного массива — подробности см. Ниже.
- Merge: это означает формирование объединенной кучи из двух разных куч — подробности см. Ниже. Две кучи должны быть как max-heap, так и min-heap. Новая куча соответствует свойству heap, в то время как исходная куча сохраняется (не стирается).
- Meld: это означает, что две кучи одного типа объединяются в новую, сохраняя дубликаты — см. Подробности ниже. Новая куча соответствует свойству heap, в то время как исходная куча уничтожается (стирается). Основное различие между объединением и объединением заключается в том, что для объединения одно дерево подходит как поддерево к корню другого дерева, что позволяет дублировать значения в новом дереве, а для объединения формируется новое дерево кучи, удаляя дубликаты. Нет необходимости поддерживать две исходные кучи слиянием.
Основные операции с кучей
- find_max (find_min): найдите максимальное значение в массиве max-heap и верните копию или найдите минимальное значение в массиве min-heap и верните копию.
- Insert: добавить новый элемент в массив кучи и переупорядочить массив, чтобы сохранить свойство кучи схемы.
- extract_max (extract_min): найти максимальное значение в массиве max-heap, удалить и вернуть его; или найдите минимальное значение в массиве min-heap, удалите и верните его.
- delete_max (delete_min): найдите корневой узел max-heap, который является первым элементом массива max-heap, удалите его, не обязательно возвращая его; или найдите корневой узел min-heap, который является первым элементом массива min-heap, удалите его, не обязательно возвращая его;
Replace: найдите корневой узел любой кучи, удалите его и замените новым. Неважно, будет ли возвращен старый root.
Операции с внутренней кучей
increase_key (decrease_key): увеличить значение любого узла для максимальной кучи и переупорядочить, чтобы сохранить свойство кучи, или уменьшить значение любого узла для минимальной кучи и переупорядочить, чтобы сохранить свойство кучи.
- Delete: удалить любой узел, затем изменить порядок, чтобы свойство кучи сохранялось для максимальной или минимальной кучи.
- shift_up: перемещать узел вверх в max-heap или min-heap на столько, сколько необходимо, переставляя для сохранения свойства кучи.
- shift_down: переместить узел вниз в max-heap или min-heap на столько, сколько необходимо, переставляя для сохранения свойства кучи.
Осмотр кучи
Size: возвращает количество ключей (значений) в куче; он не включает пустые места массива кучи. Куча может быть представлена кодом, как на схеме, или массивом.
is_empty: возвращает логическое значение true, если в куче нет узла, или логическое значение false, если в куче есть хотя бы один узел.
Просеивание в кучу
Есть отсеивание и отсеивание:
Sift-Up: это означает обмен узла с его родителем. Если свойство кучи не выполняется, замените родительский элемент на его собственный. Продолжайте этот путь по пути, пока не будет выполнено свойство heap. Процедура может достичь корня.
Sift-Down: это означает обмен узла большого значения с меньшим из двух его дочерних элементов (или одним дочерним элементом для почти полной кучи). Если свойство кучи не удовлетворяется, замените нижний узел меньшим узлом двух его собственных дочерних узлов. Продолжайте этот путь по пути, пока не будет выполнено свойство heap. Процедура может дойти до листа.
Нагромождение
Heapify означает сортировку несортированного массива, чтобы свойство кучи было удовлетворено для max-heap или min-heap. Это означает, что в новом массиве могут быть пустые места. Основной алгоритм создания кучи max-heap или min-heap выглядит следующим образом:
- если корневой узел более крайний, чем любой из его дочерних узлов, то поменяйте корень с менее крайним дочерним узлом.
- Повторите этот шаг с дочерними узлами в схеме обхода дерева предварительного заказа.
Последнее дерево — это дерево кучи, удовлетворяющее свойству кучи. Куча может быть представлена в виде древовидной диаграммы или массива. Полученная куча представляет собой частично отсортированное дерево, то есть частично отсортированный массив.
Детали операции кучи
В этом разделе статьи подробно описаны операции с кучей.
Создание кучи деталей
create_heap
См. Выше!
heapify
См. Выше
merge
Если массивы кучи,
89, 85, 87, 84, 82, 79, 73, 80, 81, , , 65, 69
и
89, 85, 84, 73, 79, 80, 83, 65, 68, 70, 71
объединены, результат без дубликатов может быть,
89, 85, 87, 84, 82, 83, 81, 80, 79, , 73, 68, 65, 69, 70, 71
После некоторого просеивания. Обратите внимание, что в первом массиве 82 нет дочерних элементов. В результирующем массиве он находится под индексом 4; и его позиции с индексом 2 (4) + 1 = 9 и 2 (4) + 2 = 10 свободны. Это означает, что у него также нет дочерних элементов на новой древовидной диаграмме. Исходные две кучи не следует удалять, поскольку их информация на самом деле не находится в новой куче (новом массиве). Базовый алгоритм объединения куч одного типа следующий:
- Присоедините один массив к основанию другого массива.
- Heapify удаляет дубликаты, следя за тем, чтобы узлы, у которых не было дочерних элементов в исходной куче, по-прежнему не имели дочерних элементов в новой куче.
meld
Алгоритм объединения двух куч одного типа (двух максимальных или двух минимальных) выглядит следующим образом:
- Сравните два корневых узла.
- Сделайте менее крайний корень и остальную часть его дерева (поддерево) вторым потомком крайнего корня.
- Просеять заблудшего потомка корня теперь крайнего поддерева, вниз в крайнем поддереве.
Полученная куча по-прежнему соответствует свойству кучи, в то время как исходная куча уничтожается (стирается). Исходные кучи могут быть уничтожены, потому что вся информация, которой они владеют, все еще находится в новой куче.
Основные операции с кучей
find_max (find_min)
Это означает найти максимальное значение в массиве max-heap и вернуть копию или найти минимальное значение в массиве min-heap и вернуть копию. Массив кучи по определению уже удовлетворяет свойству кучи. Итак, просто верните копию первого элемента массива.
insert
Это означает добавление нового элемента в массив кучи и перестановку массива таким образом, чтобы свойство кучи диаграммы сохранялось (удовлетворялось). Алгоритм этого для обоих типов куч следующий:
- Предположим полное двоичное дерево. Это означает, что при необходимости массив должен быть заполнен в конце пустыми ячейками. Общее количество узлов в полной куче — 1, или 3, или 7, или 15, или 31 и т. д .; продолжайте удваивать и прибавлять 1.
- Поместите узел в наиболее подходящее по величине пустое место, ближе к концу кучи (ближе к концу массива кучи). Если пустого места нет, начните новую строку снизу слева.
- При необходимости просеять, пока не будут удовлетворены свойства кучи.
extract_max (extract_min)
Найдите максимальное значение в массиве max-heap, удалите и верните его; или найдите минимальное значение в массиве min-heap, удалите и верните его. Алгоритм для extract_max (extract_min) следующий:
- Удалите корневой узел.
- Возьмите (удалите) крайний нижний правый узел (последний узел в массиве) и поместите в корень.
- Просеивайте по мере необходимости, пока не будет удовлетворено свойство кучи.
delete_max (delete_min)
Найдите корневой узел max-heap, который является первым элементом массива max-heap, удалите его, не обязательно возвращая его; или найдите корневой узел min-heap, который является первым элементом массива min-heap, удалите его, не обязательно возвращая его. Алгоритм удаления корневого узла следующий:
- Удалите корневой узел.
- Возьмите (удалите) крайний нижний правый узел (последний узел в массиве) и поместите в корень.
- Просеивайте по мере необходимости, пока не будет удовлетворено свойство кучи.
replace
Найдите корневой узел любой кучи, удалите его и замените новым. Неважно, будет ли возвращен старый root. При необходимости просеивайте, пока свойство кучи не будет удовлетворено.
Операции с внутренней кучей
increase_key (decrease_key)
Увеличьте значение любого узла для максимальной кучи и измените порядок, чтобы сохранить свойство кучи, или уменьшите значение любого узла для минимальной кучи и перегруппируйте, чтобы сохранить свойство кучи. Просеивайте вверх или вниз по мере необходимости, пока не будет выполнено свойство heap.
delete
Удалите интересующий узел, затем переставьте его так, чтобы свойство кучи сохранялось для максимальной или минимальной кучи. Алгоритм удаления узла следующий:
- Удалите интересующий узел.
- Возьмите (удалите) крайний нижний правый узел (последний узел в массиве) и поместите его в индекс удаленного узла. Если удаленный узел находится в последней строке, то в этом нет необходимости.
- Просеивайте вверх или вниз по мере необходимости, пока свойство кучи не будет удовлетворено.
shift_up
Перемещайте узел вверх в max-heap или min-heap на столько, сколько необходимо, изменяя порядок для сохранения свойства heap — просеивание вверх.
shift_down
Перемещайте узел вниз в max-heap или min-heap на столько, сколько необходимо, изменяя порядок для сохранения свойства кучи — просеять вниз.
Осмотр кучи
size
См. Выше!
is_empty
См. Выше!
Другие классы куч
Куча, описанная в этой статье, может рассматриваться как основная (общая) куча. Есть и другие классы куч. Однако два, о которых вы должны знать помимо этого, — это двоичная куча и д-арная куча.
Binary Heap
Двоичная куча похожа на эту основную, но с большим количеством ограничений. В частности, двоичная куча должна быть полным деревом. Не путайте полное дерево с полным деревом.
d-ary Heap
Двоичная куча — это двухзначная куча. Куча, в которой каждый узел имеет 3 дочерних узла, представляет собой 3-местную кучу. Куча, в которой каждый узел имеет 4 дочерних узла, представляет собой 4-местную кучу и так далее. У подобной кучи есть и другие ограничения.
Вывод
Куча — это полное или почти полное двоичное дерево, удовлетворяющее свойству кучи. Свойство heap имеет 2 альтернативы: для max-heap родительский элемент должен быть равен или больше по значению, чем непосредственные дочерние элементы; для минимальной кучи родительский элемент должен иметь значение, равное или меньшее, чем непосредственные дочерние элементы. Куча может быть представлена в виде дерева или массива. Когда он представлен в массиве, корневой узел является первым узлом массива; и если узел имеет индекс n, его первый дочерний элемент в массиве имеет индекс 2n + 1, а его следующий дочерний элемент находится в индексе 2n + 2. В куче есть определенные операции, которые выполняются с массивом.
Редактор: AndreyEx





