Проблема с 4 ферзями

Задача с 4 ферзями – это хорошо известная головоломка, которая включает размещение N ферзей на шахматной доске размером N × N таким образом, чтобы никакие два ферзя не угрожали друг другу. В этой статье мы сосредоточимся на задаче с 4 ферзями, в которой мы ставим своей целью расставить четырех ферзей на шахматной доске 4 × 4.

Как решить проблему с 4 ферзями?

Чтобы решить эту проблему, мы будем использовать алгоритм обратного отслеживания. Обратное отслеживание – это метод, при котором мы исследуем все возможные решения путем постепенного построения решения и обратного отслеживания всякий раз, когда обнаруживаем, что текущее решение неверно.

Подход к решению проблемы с 4 ферзями

1. В задаче с 4 ферзями мы ставим своей целью расположить четырех ферзей (Q1, Q2, Q3, Q4) на шахматной доске 4 × 4 так, чтобы никакие две ферзя не угрожали друг другу.
2. Давайте рассмотрим размещение первого ферзи, Q1, в позиции (1, 1) на шахматной доске. Однако это ограничивает возможности размещения второй ферзи, Q2, поскольку ее нельзя поместить в ту же строку, что и Q1.
3. Рассмотрев доступные ряды, мы решили разместить Q2 на (2, 3). Однако этот выбор ограничивает возможности размещения третьего ферзя, Q3, поскольку в ряду нет свободных позиций
4. В этой ситуации нам нужно вернуться к предыдущему шагу и пересмотреть размещение Q2. Мы перемещаем Q2 на позицию (2, 4), и теперь находим подходящую позицию для Q3 в (3, 2). Однако такое размещение не оставляет вариантов для размещения четвертого ферзи, Q4.
5. Мы снова возвращаемся к размещению Q1 и изменяем его на (1, 2) вместо (1, 1). Внеся эту корректировку, мы можем безопасно поместить Q2 в (2, 4), Q3 в (3, 1) и Q4 в (4, 3).
6. Таким образом, мы получаем решение (2, 4, 1, 3), которое представляет позиции четырех ферзей на шахматной доске. Это одно из возможных решений задачи с 4 ферзями. Чтобы найти альтернативные решения, нам нужно вернуться назад и изучить все возможные частичные решения.

Другим возможным решением проблемы с 4 ферзями является (3, 1, 4, 2).

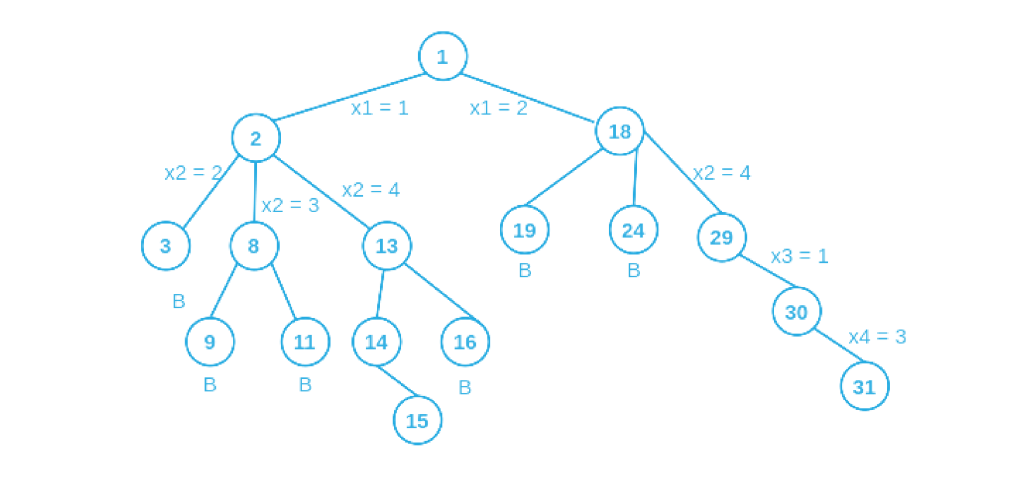
Решение задачи о 4 ферзях с использованием пространственного дерева

Для построения дерева пространства состояний мы можем использовать технику обратного отслеживания, которая позволяет нам изучить все возможные решения. Применяя этот подход, мы не только находим решения для задачи с 4 ферзями, но также можем расширить его для решения задачи с N ферзями, где N представляет любое желаемое количество ферзей.

Вот пошаговая логика для создания дерева пространства состояний:

1. Начните с рассмотрения каждой позиции (столбца) в текущей строке.
2. Проверьте все предыдущие строки, чтобы определить, есть ли уже ферзь, помещенная в какой-либо из столбцов.
3. Кроме того, проверьте предыдущие диагональные столбцы, чтобы убедиться, что в любой из этих позиций есть ферзь.
4. Если выполняется любое из этих условий, указывающее на то, что две ферзя будут атаковать друг друга, вернитесь к предыдущему ряду и переместите предыдущего ферзя на шаг вперед.
5. Если ни одна из предыдущих позиций не конфликтует, поместите текущий ферзь в текущую позицию и перейдите к следующему ряду.

Следуя этой процедуре, мы можем систематически исследовать пространство состояний, расширяясь с каждым решением и возвращаясь к нему всякий раз, когда это необходимо. Это позволяет нам найти все возможные решения для задачи с N ферзями, а не только для задачи с 4 ферзями. Дерево пространства состояний обеспечивает визуальное представление процесса принятия решений и изучение различных путей для достижения обоснованных решений. Каждый узел в дереве представляет определенную конфигурацию ферзей на шахматной доске, в то время как ребра представляют решения, принятые для достижения этой конфигурации. С помощью этого метода мы можем выполнить исчерпывающий поиск в пространстве состояний, чтобы найти все допустимые решения задачи с N ферзьми, где N может быть любым желаемым количеством ферзей.

Реализация проблемы с 4 ферзями на C ++

Проблема с 4 ферзями

#include 
using namespace std;
int a[30], cnt;
int place(int pos)
{
    int i;
    for (i = 1; i < pos; i++) {
        if ((a[i] == a[pos])
            || ((abs(a[i] - a[pos]) == abs(i - pos))))
            return 0;
    }
    return 1;
}
void print_sol(int N)
{
    int i, j;
    cnt++;
    cout << "\n\nSolution " << cnt << ":\n";
    for (i = 1; i <= N; i++) {
        for (j = 1; j <= N; j++) {
            if (a[i] == j)
                cout << "Q\t";
            else
                cout << "*\t";
        }
        cout << endl;
    }
}
void queen(int n)
{
    cnt = 0;
    int k = 1;
    a[k] = 0;
    while (k != 0) {
        a[k] = a[k] + 1;
        while ((a[k] <= n) && !place(k))
            a[k]++;
        if (a[k] <= n) {
            if (k == n)
                print_sol(n);
            else {
                k++;
                a[k] = 0;
            }
        }
        else
            k--;
    }
}
int main()
{
    int N = 4;
    queen(N);
    cout << "\nTotal solutions=" << cnt;
    return 0;
}

Заключение

В заключение, задача с 4 ферзями предполагает размещение четырех ферзей на шахматной доске 4 × 4 так, чтобы они не угрожали друг другу. Используя отслеживание назад, мы можем систематически исследовать все возможные решения. Этот подход может быть расширен для решения проблемы с N ферзьми. Понимая концепции и реализуя предоставленный код, мы можем эффективно находить допустимые места размещения ферзей. Задача с 4 ферзями служит отправной точкой для решения более крупных задач и изучения комбинаторной оптимизации.

Часто задаваемые вопросы (FAQs)

Вопрос 1. В чем проблема с 4 ферзями?
Задача с 4 ферзями предполагает размещение четырех ферзей на шахматной доске 4 × 4 таким образом, чтобы никакие два ферзи не угрожали друг другу.

Вопрос 2. Как я могу решить проблему с 4 ферзями?
Один из подходов заключается в использовании алгоритма обратного отслеживания. Начните с размещения первого ферзя, а затем рекурсивно исследуйте все возможные позиции для оставшихся ферзей, возвращаясь при возникновении конфликтов.

Вопрос 3. Можно ли решить задачу с 4 ферзями, используя доску другого размера?
Да, размер шахматной доски можно отрегулировать для решения задачи с N ферзями. Например, при N = 8 будет использоваться шахматная доска 8 × 8.

Вопрос 4. Существует ли несколько решений проблемы с 4 ферзями?
Да, проблема с 4 ферзьми может иметь несколько допустимых решений. Отслеживание назад помогает исследовать различные пути и находить альтернативные места размещения ферзей.

Вопрос 5. Является ли алгоритм обратного отслеживания наиболее эффективным способом решения проблемы с 4 ферзями?
Алгоритм обратного отслеживания подходит для задач небольшого размера. Однако для более крупных задач с N ферзьми могут потребоваться более оптимизированные методы, такие как обрезка или дополнительные ограничения для повышения эффективности.

(1 оценок, среднее: 5,00 из 5)

Загрузка...