Алгоритм Крускала
Граф, не имеющий направлений, называется неориентированным графом. Каждый граф должен иметь путь от одного узла к другому узлу. Остовное дерево также является неориентированным связным графом, в котором присутствуют все узлы графа с минимальным количеством ребер. Если остовное дерево не имеет всех узлов графа, то мы не можем сказать, что это остовное дерево. Суммарные веса остовного дерева будут меньше исходного веса графа, так как мы соединили его через ребра минимального веса. Остовное дерево также не имеет цикла. Любой граф имеет более одного остовного дерева, но только одно из них будет уникальным. Мы называем это минимальным остовным деревом, поскольку пытаемся создать полный граф со всеми узлами, сохраняя при этом низкий вес.
Пример:
Давайте разберемся с минимальным остовным деревом на примере.
Итак, как мы знаем, минимальное остовное дерево является частью графа, но с меньшими затратами. Таким образом, этот сценарий можно проиллюстрировать на примере.
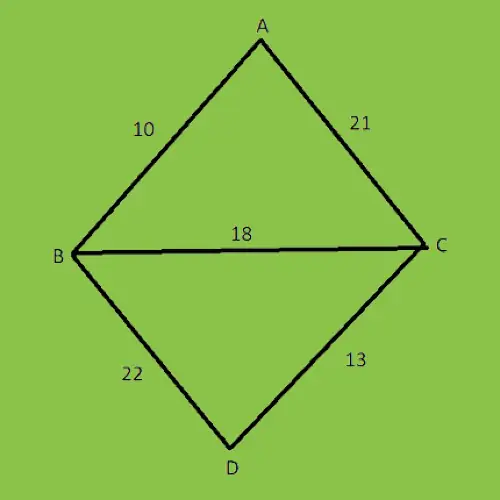
Предположим, у нас есть такой график.
Приведенный выше граф можно упорядочить по-разному, так что цикл графа будет удален, иначе он не будет MST (минимальным остовным деревом). Итак, мы удалим цикл из графа и посчитаем общую стоимость графа. У нас есть четыре узла или вершины (A, B, C и D).
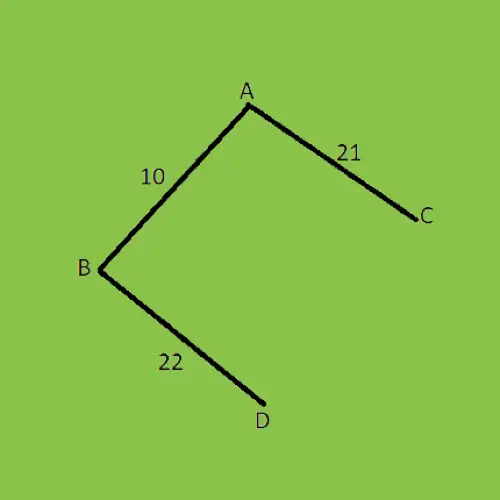
Дело 1:
После удаления цикла из графа указанная выше стоимость графа MST (минимальное остовное дерево) составляет 56.
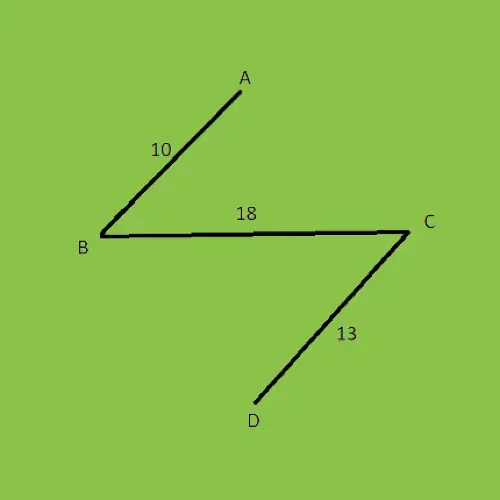
Случай -2:
После удаления цикла из графа указанная выше стоимость графа MST (минимальное остовное дерево) составляет 53.
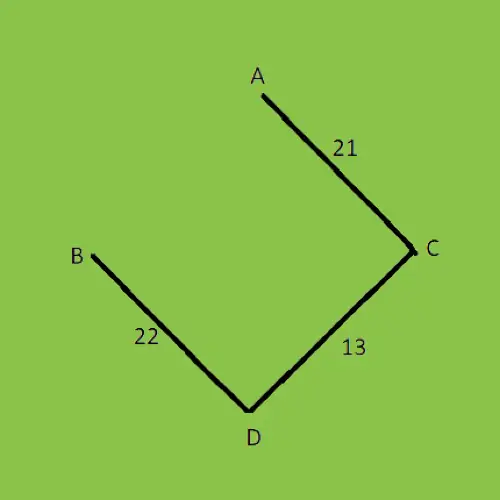
Случай – 3:
После удаления цикла из графа указанная выше стоимость графа MST (минимальное остовное дерево) составляет 41.
Мы видим, что последний график общей стоимости варианта 3 намного ниже по сравнению с двумя другими графиками. Таким образом, этот граф является нашим окончательным MST (минимальным остовным деревом) для исходного графа. Алгоритмы Прима или Крускала преследуют цель найти как можно более низкую стоимость графа. Так что наша цель в этой статье объяснить этот MST.
Мы можем нарисовать остовное дерево с помощью следующих двух методов:
- Алгоритм Крускала
- Алгоритм Прима
В этой статье мы собираемся обсудить алгоритм Крускала.
Алгоритм Крускала:
Алгоритм Крускала очень легко реализовать по сравнению с алгоритмом Прима, потому что в этом алгоритме нам не нужно заботиться о вершинах смежности. В этом алгоритме алгоритм Крускала стартует со всех вершин графа. Мы выбираем вершину ребра минимального веса и начинаем создавать минимальное остовное дерево. Мы выбираем другое ребро с минимальным весом и добавляем его в минимальное остовное дерево. Этот процесс продолжается до тех пор, пока мы не добавим все узлы исходного графа. Как только все узлы графа будут добавлены к минимальному остовному дереву, алгоритм остановится. При создании минимального остовного дерева графа мы также должны позаботиться об этом графе, не создавая никаких циклов, потому что циклов не должно быть в минимальном остовном дереве.
Таким образом, если какой-либо узел создает цикл в минимальном остовном дереве, мы выбираем другой узел, даже если вес этого узла больше, чем вес предыдущего узла, создавшего цикл.
Алгоритм Крускала отличается от алгоритма Прима. Алгоритм Прима при создании минимального остовного дерева начинается с любого узла или вершины, а затем добавляет еще один узел или вершину только из узлов смежности. Но алгоритм Крускала не заботится о узле смежности и всегда выбирает тот узел, который имеет меньший вес, но этот узел не должен создавать цикл в минимальном остовном дереве.
Шаги алгоритма Крускала:
При написании кода C++ для алгоритма Крускала предпринимаются следующие шаги.
Шаг 1 : Мы создаем массив для хранения групп узлов или вершин графа.
Шаг 2 : Мы создаем еще один массив для хранения весов ребер графа.
Шаг 3 : Для остовного дерева мы создаем новый массив.
Шаг 4 : Мы располагаем массив ребер в порядке возрастания.
Шаг 5 : Повторяем шаг 6 до тех пор, пока массив отсортированных весов ребер не станет пустым.
Шаг 6 : Мы сравниваем две группы бок о бок. В этом случае, если один узел группы не соответствует другому узлу, мы добавляем это ребро в остовное дерево и добавляем его в ту же группу.
Шаг 7. Переберите все ребра остовного дерева, чтобы определить его общий вес.
Пример:
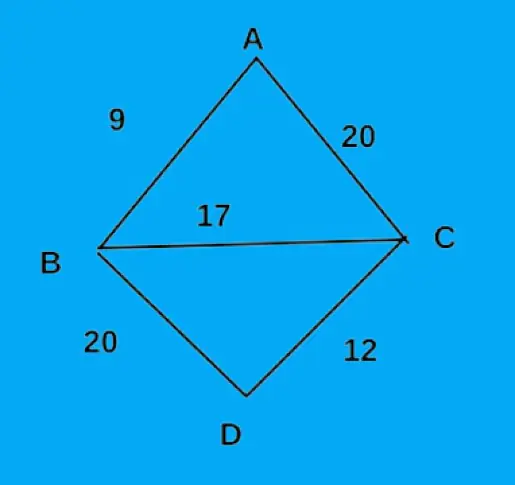
Теперь мы реализуем описанные выше шаги алгоритма на примере. У нас есть приведенный ниже график, и мы найдем минимальное остовное дерево для этого графа.
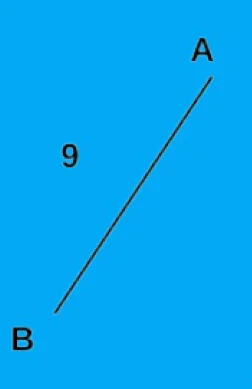
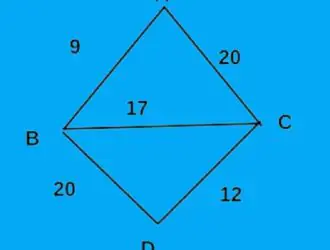
Итак, согласно алгоритму, мы сначала выбираем ребро с наименьшим весом, которым является AB. Поэтому мы выбрали это ребро и сохранили его в массиве связующего дерева. Вес ребра AB равен 9.
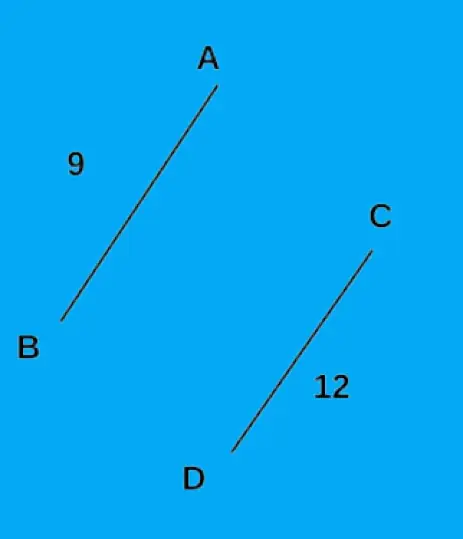
Теперь мы выбираем ребро следующего наименьшего веса, CD, и сохраняем это ребро в массиве минимального остовного дерева. Вес ребра компакт-диска равен 12.
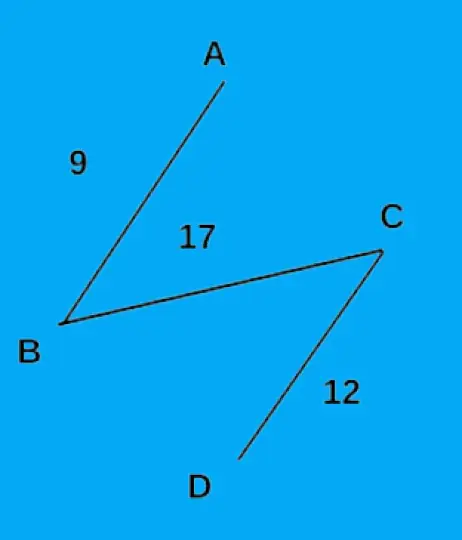
Следующим наименьшим ребром, которое мы получили, было BC, которое мы сохранили в массиве. Взвешенное ребро BC равно 17.
Наш алгоритм остановится здесь, потому что у нас есть все вершины графа и минимальное остовное дерево. Общий вес этого MST равен 9 + 12 + 17 = 38.
Программа : Ниже приведен код C++ для алгоритма Крускала.
#include #include #include class EdgeGraph { public: int nodeSTART; int nodeEND; int wght; EdgeGraph(){} EdgeGraph(int node_1, int node_2, int weight): nodeSTART(node_1), nodeEND(node_2), wght(weight){} }; bool CompareEdgeCost (const EdgeGraph a, const EdgeGraph b) { return a.wght < b.wght; } class G{ private: int num_of_nodes; std :: vector EdgeGraphlist; std :: vector parentNode; std :: vector rankNode; public: G(){} G (int num_of_nodes) { this->num_of_nodes = num_of_nodes; parentNode.resize(num_of_nodes); rankNode.resize(num_of_nodes); } void AddEdgeGraph(EdgeGraph e); int FindparentNode(int node); void KruskalMST_ALGO(std :: vector&); void DisplayEdgeGraphs(std :: vector&); }; void G :: AddEdgeGraph (EdgeGraph e) { EdgeGraphlist.push_back(e); } int G :: FindparentNode (int node) { if ( node != parentNode[node] ) parentNode[node] = FindparentNode(parentNode[node]); return parentNode[node]; } void G :: DisplayEdgeGraphs (std :: vector& mst) { int cost = 0; std :: cout << "EdgeGraphs of MST : "; for (auto& e : mst) { std :: cout << "[" << e.nodeSTART << "-" << e.nodeEND << "](" << e.wght << ") "; cost += e.wght; } std :: cout << "\n Kruskal MST Cost : " << cost << std :: endl; } //Это основная функция алгоритма Крускала, которая выполняет поиск // минимального связующего дерева. void G :: KruskalMST_ALGO (std :: vector& result) { for (int i=0; i<num_of_nodes; i++) { parentNode[i] = i; rankNode[i] = 0; } sort(EdgeGraphlist.begin(), EdgeGraphlist.end(), CompareEdgeCost); for (auto& e : EdgeGraphlist) { int root_1 = FindparentNode(e.nodeSTART); int root_2 = FindparentNode(e.nodeEND); if (root_1 != root_2) { result.push_back(e); if (rankNode[root_1] < rankNode[root_2]) { parentNode[root_1] = root_2; rankNode[root_2]++; } else { parentNode[root_2] = root_1; rankNode[root_1]++; } } } } int main() { int num_of_nodes = 6; // (0, 1, 2, 3, 4, 5) EdgeGraph e1(0, 1, 4); EdgeGraph e2(0, 2, 1); EdgeGraph e3(0, 3, 5); EdgeGraph e4(1, 3, 2); EdgeGraph e5(1, 4, 3); EdgeGraph e6(1, 5, 3); EdgeGraph e7(2, 3, 2); EdgeGraph e8(2, 4, 8); EdgeGraph e9(3, 4, 1); EdgeGraph e10(4, 5, 3); G g1(num_of_nodes); g1.AddEdgeGraph(e1); g1.AddEdgeGraph(e2); g1.AddEdgeGraph(e3); g1.AddEdgeGraph(e4); g1.AddEdgeGraph(e5); g1.AddEdgeGraph(e6); g1.AddEdgeGraph(e7); g1.AddEdgeGraph(e8); g1.AddEdgeGraph(e9); g1.AddEdgeGraph(e10); std :: vector mst; // Это сохранит минимальное связующее дерево g1.KruskalMST_ALGO(mst); g1.DisplayEdgeGraphs(mst); return 0; }
Выход :
EdgeGraphs of MST : [0-2](1) [3-4](1) [1-3](2) [2-3](2) [1-5](3)
Kruskal MST Cost : 9
Заключение
Мы изучили минимальное остовное дерево Крускала, которое большинство людей предпочитает в первую очередь, когда им нужно найти граф MST из графа. Алгоритм Крускала легко понять и реализовать в реальном приложении. Как и алгоритм Прима, алгоритм Крускала также очень полезен в реальных приложениях. Итак, мы должны понять этот алгоритм.
Редактор: AndreyEx