Алгоритм Прима
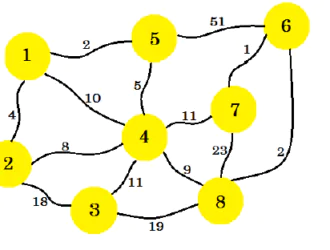
Минимальное связующее дерево:
Граф, не имеющий направлений, называется неориентированным графом. Каждый граф должен иметь путь от одного узла к другому узлу. Остовное дерево также является неориентированным связным графом, в котором присутствуют все узлы графа с минимальным количеством ребер. Если остовное дерево не имеет всех узлов графа, то мы не можем сказать, что это остовное дерево. Суммарные веса остовного дерева будут меньше исходного веса графа, так как мы соединили его через ребра минимального веса. Покрывающее дерево также не имеет цикла. Любой граф имеет более одного остовного дерева, но только одно из них будет уникальным. Мы называем это минимальным остовным деревом, поскольку пытаемся создать полный граф со всеми узлами, сохраняя при этом низкий вес.
Мы можем нарисовать остовное дерево с помощью следующих двух методов:
- Алгоритм Крускала
- Алгоритм Прима
В этой статье мы собираемся обсудить алгоритм Прима. Алгоритм Крускала будет рассмотрен в следующей статье.
Алгоритм Прима:
Алгоритм Прима используется для нахождения минимального остовного дерева графа. Алгоритм примитива начинается с любого узла, а затем добавляет любой соседний узел с минимальным весом, и этот процесс продолжается до тех пор, пока не будут посещены все узлы в графах. При создании минимального остовного дерева графа мы также не должны создавать циклы, потому что циклов не должно быть в минимальном остовном дереве.
Шаги алгоритма Прима:
Алгоритм прима использует жадный подход для минимального остовного дерева. Мы должны выбрать любую вершину графа, а затем выбрать следующую вершину смежности, чей вес меньше, и мы продолжаем этот процесс до тех пор, пока не соединим все узлы графа.
- Шаг 1: Выберите любую исходную вершину в графе.
- Шаг 2: Найдите ребро минимального веса, которое примыкает к источнику, а затем соедините его с остовным деревом.
- Шаг 3: Повторяйте шаг 2, пока все узлы не будут добавлены в минимальное остовное дерево.
Пример :
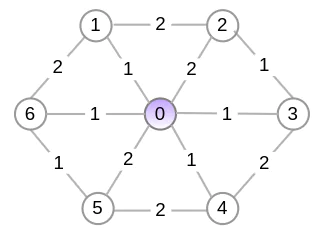
Ниже приведен пример поиска минимального остовного дерева с использованием алгоритма Прима.
1. Выбираем любой случайный узел из графа G и добавляем его в MST (минимальное остовное дерево). Мы выбираем здесь узел 0.
2. Теперь мы выбираем то ребро, которое является смежным с исходным узлом (0), но с наименьшим весом, а затем добавляем этот узел с наименьшим весом в минимальное остовное дерево.
3. Теперь мы выбираем то ребро, которое является смежным с исходным узлом (0 или 1), но с наименьшим весом, а затем добавляем этот узел с наименьшим весом в минимальное остовное дерево.
4. Теперь мы выбираем то ребро, которое является смежным с исходным узлом (0, 1 или 3), но с наименьшим весом, а затем добавляем этот узел с наименьшим весом в минимальное остовное дерево.
5. Теперь мы выбираем то ребро, которое является смежным с исходным узлом (0, 1, 3 или 4), но с наименьшим весом, а затем добавляем этот узел с наименьшим весом в минимальное остовное дерево.
6. Теперь мы выбираем то ребро, которое является смежным с исходным узлом (0, 1, 3, 4 или 6), но с наименьшим весом, а затем добавляем этот узел с наименьшим весом в минимальное остовное дерево.
7. Теперь мы выбираем то ребро, которое является смежным с исходным узлом (0, 1, 3, 4, 6 или 2), но с наименьшим весом, а затем добавляем этот узел с наименьшим весом в минимальное остовное дерево.
Выше наш окончательный MST (минимальное остовное дерево), а общая стоимость равна 6.
Программа C++ Prim MST (минимальное связующее дерево):
#include<iostream>
#include<vector>
#include<queue>
#include<algorithm>
#include<cstring>
typedef std :: pair<int,int> SII;
typedef std :: vector<SII> SSII;
int PrimsMST (int sourceNode, std :: vector<SSII> & graph){
// В этой очереди будут храниться сведения о каждом узле
// вместе с их весовой ценностью.
std :: priority_queue<SII, std :: vector<SII>, std :: greater<SII>> k;
k.push(std :: make_pair(0, sourceNode));
bool nodesAdded[graph.size()];
memset(nodesAdded, false, sizeof(bool)*graph.size());
int mst_tree_cost = 0;
while (!k.empty()) {
// We are selecting here the node which has minimum cost
SII itemNode;
itemNode = k.top();
k.pop();
int Node = itemNode.second;
int Cost = itemNode.first;
// Здесь мы проверяем, не был ли какой-либо узел добавлен в MST,
// затем добавляем этот узел.
if (!nodesAdded[Node]) {
mst_tree_cost += Cost;
nodesAdded[Node] = true;
// Выполните итерацию по узлам negibour, которые недавно были удалены
// из очереди приоритетов.
// и добавлен в MST, который еще не добавлен
for (auto & pair_node_cost : graph[Node]) {
int adjency_node = pair_node_cost.second;
if (nodesAdded[adjency_node] == false) {
k.push(pair_node_cost);
}
}
}
}
return mst_tree_cost;
}
int main(){
// Подробная информация о графике со стоимостью и узлом смежности.
SSII fromNode_0_in_graph_1 = { {1,1}, {2,2}, {1,3},
{1,4}, {2,5}, {1,6} };
SSII fromNode_1_in_graph_1 = { {1,0}, {2,2}, {2,6} };
SSII fromNode_2_in_graph_1 = { {2,0}, {2,1}, {1,3} };
SSII fromNode_3_in_graph_1 = { {1,0}, {1,2}, {2,4} };
SSII fromNode_4_in_graph_1 = { {1,0}, {2,3}, {2,5} };
SSII fromNode_5_in_graph_1 = { {2,0}, {2,4}, {1,6} };
SSII fromNode_6_in_graph_1 = { {1,0}, {2,2}, {1,5} };
int num_of_nodes = 7; // Total Nodes (0 to 6)
std :: vector<SSII> primsgraph;
primsgraph.resize(num_of_nodes);
primsgraph[0] = fromNode_0_in_graph_1;
primsgraph[1] = fromNode_1_in_graph_1;
primsgraph[2] = fromNode_2_in_graph_1;
primsgraph[3] = fromNode_3_in_graph_1;
primsgraph[4] = fromNode_4_in_graph_1;
primsgraph[5] = fromNode_5_in_graph_1;
primsgraph[6] = fromNode_6_in_graph_1;
// Как мы уже знаем, мы должны выбрать исходную вершину,
// поэтому мы начинаем с узла вершины 0.
std :: cout << "Общая стоимость минимального связующего дерева после алгоритма Прима : "
"" << PrimsMST(0, primsgraph) << std :: endl;
return 0;
}Выход:
Общая стоимость минимального связующего дерева после алгоритма Прима : 6 Process finished with exit code 0
Временная сложность алгоритма MST Prim:
- Общее время, необходимое для обработки и выбора определенного узла очереди с приоритетом, который еще не добавлен в MST, составляет logV. Но поскольку это работает для каждой вершины, общая временная сложность составляет V (logV).
- Граф неориентированный, и общее количество ребер будет 2E. Поскольку мы должны поместить узлы в приоритетную очередь, это займет журнал общего времени (V). Однако, поскольку у нас есть в общей сложности 2E ребра, наша общая операция отправки будет 2E (log (V)).
- Общая сложность после операции 1 и 2 составляет O( (E + V ) log (V )).
Заключение:
Мы изучили минимальное остовное дерево Prim, которое большинство людей предпочитает в первую очередь, когда им нужно найти граф MST из графа. Алгоритм Prim прост для понимания и реализации в реальном приложении. Алгоритм Prim очень полезен в реальных приложениях, например, при соединении железнодорожных путей с целыми городами. Так что это всего лишь один пример, но его применение огромно, поэтому мы должны понять этот алгоритм.
Редактор: AndreyEx











ниц не зрозумяле, я пердоле