ИТ Блог. Администрирование серверов на основе ядра Linux
Анализ временных рядов — это известный метод исследовательского анализа данных машинного обучения, который позволяет нам увидеть, как точки данных меняются с течением времени. Несколько формулировок задач на основе временных рядов, таких как прогноз продаж билетов, анализ цен на акции и т. д. Временные ряды могут демонстрировать различные тенденции, которые трудно проанализировать, просто взглянув на график. В результате кластеризация тенденций временного ряда является хорошей идеей. Мы рассмотрим, что такое временные ряды, что такое кластеризация и как кластеризовать данные временных рядов.
Временной ряд — это набор указателей данных, сгруппированных во времени. Точки данных представляют собой действие, которое происходит в течение определенного периода времени. Типичным примером является общее количество акций, торгуемых за заданный интервал времени, наряду с другими параметрами, такими как цены акций и их соответствующая торговая информация в каждую секунду. В отличие от переменной с непрерывным временем, эти точки данных временного ряда имеют дискретные значения в различные моменты времени. В результате часто используются дискретные переменные данных. Данные для временного ряда можно собирать за любой период времени, от нескольких минут до нескольких лет. Время, в течение которого собираются данные, не имеет нижнего или верхнего предела. В машинном обучении и глубоком обучении существуют различные проблемы прогнозирования на основе временных рядов, такие как прогнозирование цены акций компании, распознавание человеческой деятельности, предсказание количества авиабилетов и т. д. Это экономит много денег и помогает компаниям принимать взвешенные решения, прежде чем инвестировать во что-то. Примерный график, приведенный ниже, показывает изменение наблюдений во времени.
Кластеризация — это метод машинного обучения без учителя. Выводы получаются из наборов данных, которые не имеют помеченных выходных переменных в методе обучения без учителя. Это тип исследовательского анализа данных, который позволяет нам рассматривать многомерные наборы данных.
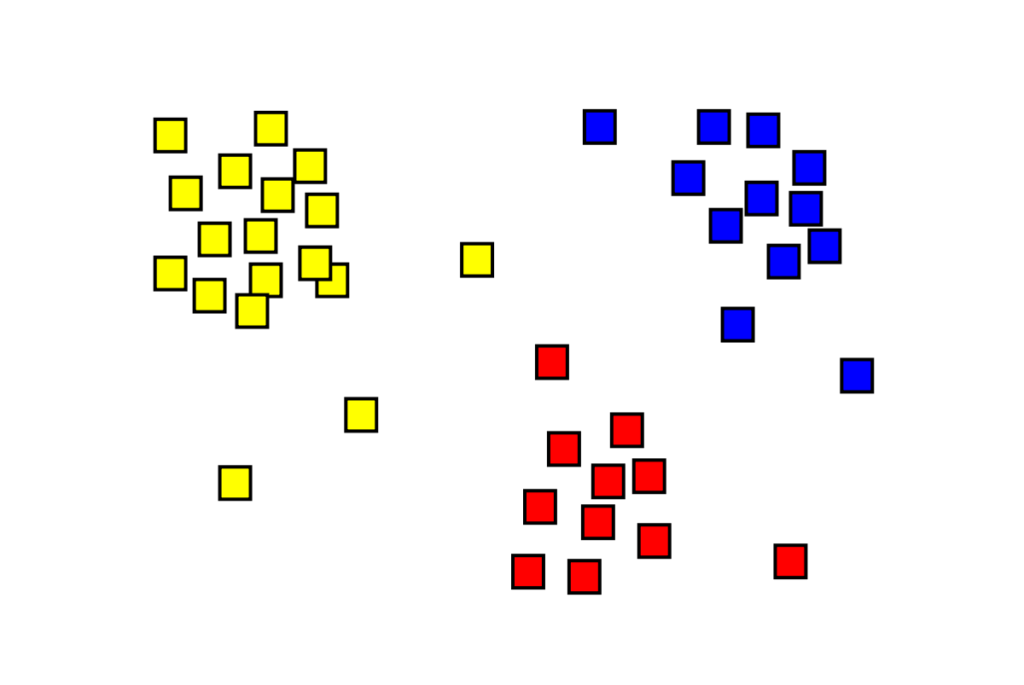
Кластеризация — это машинное обучение или математический подход, при котором точки данных группируются в определенное количество кластеров со схожими характеристиками среди точек данных внутри каждого кластера. Кластеры состоят из точек данных, сгруппированных вместе, так что пространство между ними сведено к минимуму. Способ создания кластеров определяется типом выбранного нами алгоритма. Поскольку не существует критерия хорошей кластеризации, выводы, сделанные из наборов данных, также зависят от того, что и как пользователь разрабатывает алгоритм кластеризации. Кластеризацию можно использовать для решения таких задач, как сегментация клиентов, рекомендательные системы, обнаружение аномалий и так далее. Вам может быть знаком подход кластеризации k-средних, в котором у нас нет меток и мы должны поместить каждую точку данных в свой собственный кластер. Известным подходом к кластеризации являются K-средние. На рисунке ниже показано, как мы группируем разные точки данных с одинаковыми функциями в один и тот же кластер.
Метод кластеризации временных рядов — это неконтролируемый подход к обработке данных для классификации точек данных на основе их сходства. Цель состоит в том, чтобы максимизировать сходство данных между кластерами, минимизируя его. Базовым методом в науке о данных для выявления аномалий и обнаружения закономерностей является кластеризация временных рядов, которая используется в качестве подпрограммы для других более сложных алгоритмов. Этот метод особенно полезен при анализе тенденций в очень больших наборах данных временных рядов. Мы не можем различать тенденции, просто глядя на график временного ряда. Здесь вы можете сгруппировать тенденции. Затем различные тенденции будут сгруппированы в разные кластеры.
Метод ядра относится к преобразованию данных в другое измерение с четким разделительным краем между нелинейно разделяемыми группами данных. Метод ядра k-средних использует тот же прием, что и метод k-средних, за исключением того, что метод ядра используется для вычисления расстояния вместо евклидова расстояния. Применительно к алгоритму ядерный подход может находить нелинейные структуры и лучше всего подходит для реальных наборов данных.
Наиболее частым методом кластеризации временных рядов является K-среднее. Обычный подход состоит в том, чтобы свести данные временных рядов в двумерный массив, где каждый столбец соответствует каждому временному индексу, а затем использовать стандартные алгоритмы кластеризации, такие как k-mean, для кластеризации данных. Однако измерения расстояния типичными алгоритмами кластеризации, такие как евклидово расстояние, часто не подходят для временных рядов. Предпочтительным способом является использование метрики для сравнения тенденций временного ряда вместо меры расстояния по умолчанию. Одним из самых популярных методов, используемых для этого, является Dynamic Time Warping.
Несмотря на то, что один сигнал сдвинут во времени относительно другого, Dynamic Time Warping позволяет системе сравнивать два сигнала и искать сходство. Его способность проверять наличие известных речевых артефактов независимо от темпа речи говорящего делает его полезным и для задач распознавания речи. Например, если есть два массива: [1, 2, 3] и [4, 5, 6], вычислить расстояние между ними несложно, так как вы можете просто выполнить поэлементное вычитание и сложить все различия. Однако это будет непросто, если размер массивов разный. Мы можем рассматривать эти массивы как последовательность сигналов. Компонент «Динамический» предполагает, что последовательность сигналов можно перемещать вперед и назад для поиска соответствия, не ускоряя и не замедляя всю последовательность. Если Time Warping растягивает или сжимает резинку, DTW расширяет или сжимает эту резинку, чтобы она соответствовала контурам поверхности. Ниже представлено визуальное представление DTW.
from fastdtw import fastdtw from scipy.spatial.distance import euclidean sig1 = np.array([1, 2, 3, 4]) sig2 = np.array([1, 2, 2, 4, 4, 5]) distance, path = fastdtw(sig1, sig2, dist=euclidean) print(distance) print(path)
В этой статье было рассмотрено определение временных рядов, кластеризация и объединение этих двух тенденций для кластеризации временных рядов. Мы рассмотрели популярный метод для этого, называемый Dynamic Time Warping (DTW), а также процессы и реализацию, связанные с его использованием.
(1 оценок, среднее: 5,00 из 5)
Загрузка...
