Основные графовые алгоритмы встречаются на собеседованиях по программированию

В начале изучения графовые алгоритмы могут показаться пугающими, но как только вы поймете фундаментальные алгоритмы обхода, шаблоны и потренируетесь в решении нескольких задач, они станут намного проще.

В этой статье мы рассмотрим 10 наиболее распространённых алгоритмов и шаблонов для работы с графами, которые встречаются на собеседованиях по программированию. Мы объясним, как они работают, когда их следует использовать, как их реализовать.

1. Поиск в глубину (DFS)

Поиск в глубину (DFS)

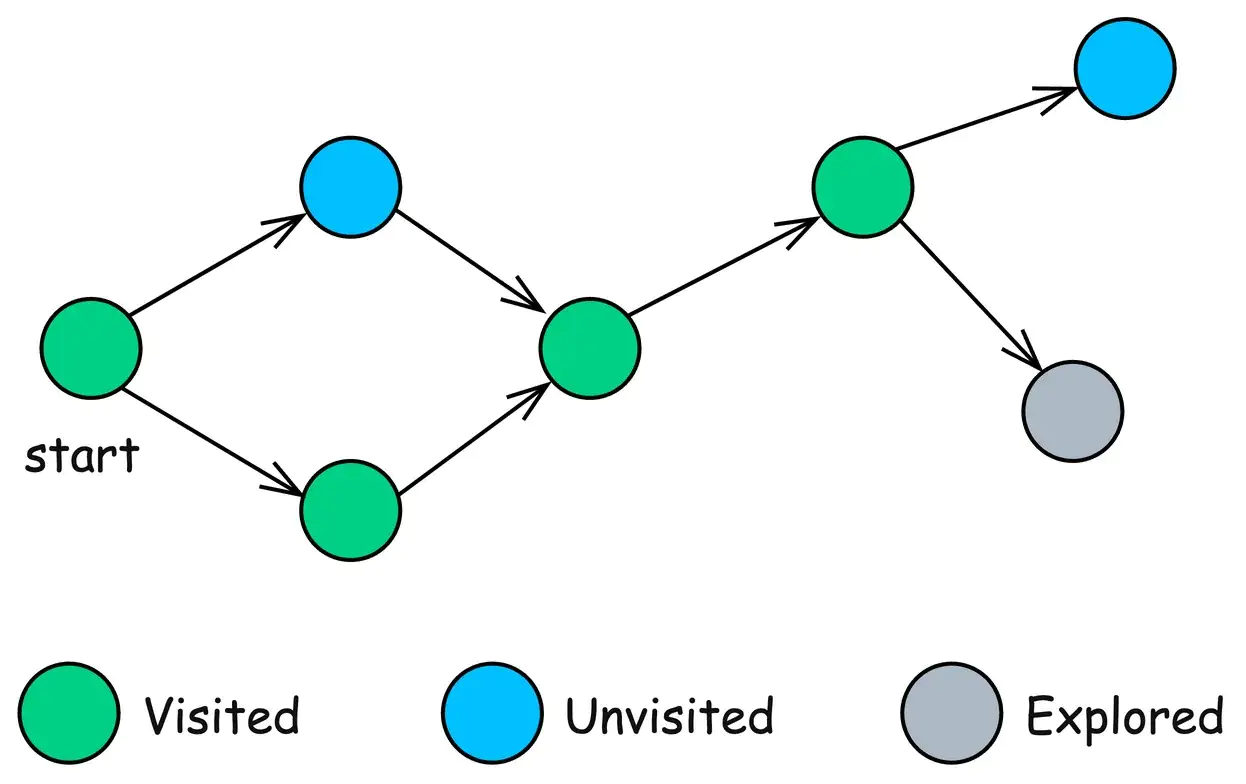
DFS — это фундаментальный алгоритм обхода графа, используемый для систематического изучения узлов и ребер графа.

Он начинается с заданного корневого узла и исследует как можно дальше вдоль каждой ветви, прежде чем вернуться назад.

DFS особенно полезен в таких сценариях, как:

• Найдите путь между двумя узлами.
• Проверка, содержит ли граф какие-либо циклы.
• Идентификация изолированных подграфов в более крупном графе.
• Топологическая сортировка: планирование задач без нарушения зависимостей.

Как работает DFS:

• Начните с корневого узла: Отметьте начальный узел как посещённый.
• Изучите соседние узлы: Для каждого соседнего узла выполните следующее:
  • Если сосед не был посещён, выполните для него рекурсивную DFS.
• Возврат: после изучения всех путей от узла вернитесь к предыдущему узлу и продолжите процесс.
• Завершение: Алгоритм завершается, когда посещены все узлы, достижимые из начального узла.

Реализация:

Рекурсивная DFS: использует системную рекурсию (стек вызовов функций) для возврата к предыдущему состоянию.

def dfs_recursive(graph, node, visited=None):
    if visited is None:
        visited = set()
    visited.add(node)
    print(f"Посещение {node}")
    for neighbor in graph[node]:
        if neighbor not in visited:
            dfs_recursive(graph, neighbor, visited)
    return visited

Объяснение:

• Базовый вариант: Если visited не указан, инициализируйте его.
• Посетите узел: добавьте текущий узел в набор visited.
• Рекурсивный вызов: для каждого непосещенного соседа выполните рекурсивный вызов dfs_recursive.

Итеративная DFS: использует явный стек для имитации поведения при вызове функции.

def dfs_iterative(graph, start):
    visited = set()
    stack = [start]
    while stack:
        node = stack.pop()
        if node not in visited:
            visited.add(node)
            print(f"Посещение {node}")
            # Добавление соседей в стек
            stack.extend([сосед за соседом в graph[node] если сосед не в гостях])
    return visited

Объяснение:

• Инициализировать:
  • A visited набор для отслеживания посещенных узлов.
  • A stack с начальным узлом.
• Узлы процесса:
  • Извлеките узел из стека.
  • Если никто не посещен, отметьте как посещенный и добавьте его соседей в стек.

Временная сложность: O(V + E), где V — количество вершин, а E — количество рёбер. Это связано с тем, что алгоритм посещает каждую вершину и каждое ребро по одному разу.

Сложность по памяти: O(V), из-заиспользования стека для рекурсии (при рекурсивной реализации) или явного стека (при итеративной реализации).

2. Поиск по ширине (BFS)

Поиск по ширине (BFS)

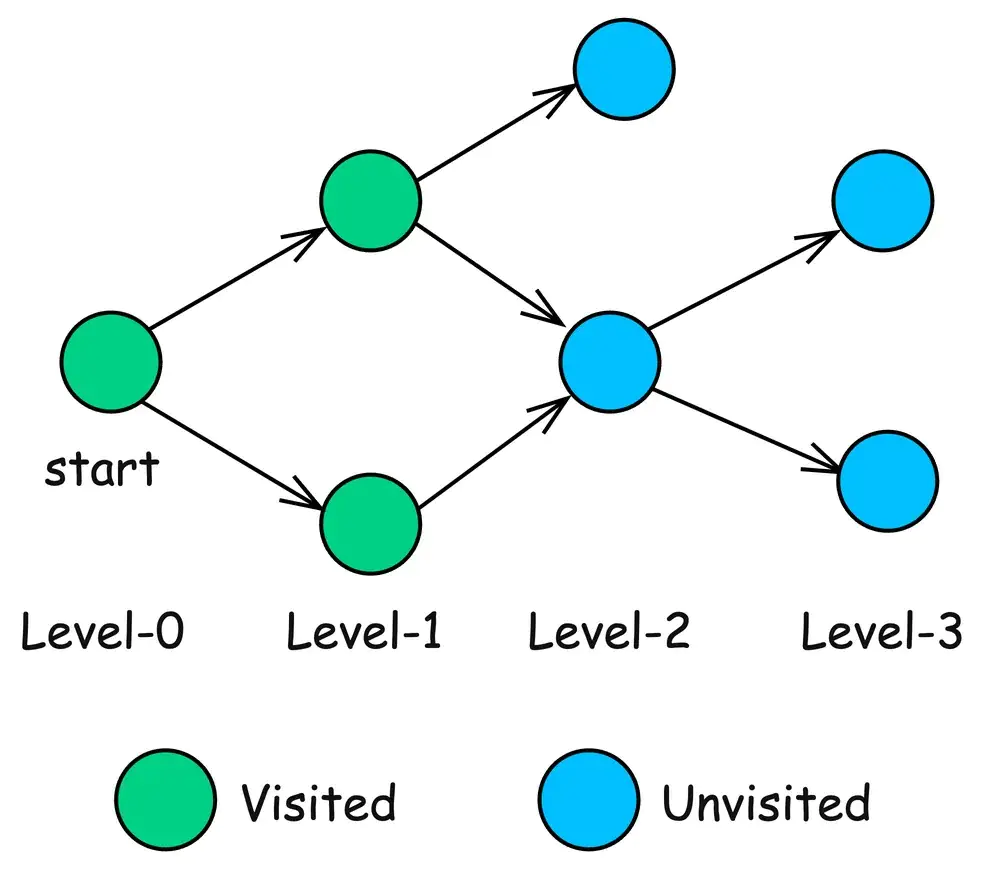
BFS — это фундаментальный алгоритм обхода графа, который систематически исследует вершины графа уровень за уровнем.

Начиная с выбранного узла, BFS сначала посещает все его непосредственные соседние узлы, а затем переходит к соседним узлам этих соседних узлов. Это гарантирует, что узлы будут исследованы в порядке их удалённости от начального узла.

BFS особенно полезен в таких сценариях, как:

• Нахождение минимального количества ребер между двумя узлами.
• Обработка узлов в иерархическом порядке, как в древовидных структурах данных.
• Поиск людей с определенной степенью связи в социальной сети.

Как работает BFS:

1. Инициализация: создайте очередь и поместите в неё начальный узел.
   • Отметьте начальный узел как посещенный.
2. Цикл обхода: Пока очередь не пуста:
   • Удаление узла из очереди в начале очереди.
   • Посетите всех непрошеных соседей:
     • Отметьте каждого соседа как посещенного.
     • Поставьте соседа в очередь.
3. Завершение: Алгоритм завершается, когда очередь пуста, то есть все достижимые узлы посещены.

Реализация:

from collections import deque

def bfs(graph, start):
    visited = set()
    queue = deque([start])
    visited.add(start)
    while queue:
        vertex = queue.popleft()
        print(f"Посещение {vertex}")
        for neighbor in graph[vertex]:
            if neighbor not in visited:
                visited.add(neighbor)
                queue.append(neighbor)

Временная сложность: O(V + E), где V — количество вершин, а E — количество рёбер. Это связано с тем, что BFS посещает каждую вершину и ребро ровно один раз.

Сложность по памяти: O(V)для очереди и набора посещённых элементов, используемых для обхода.

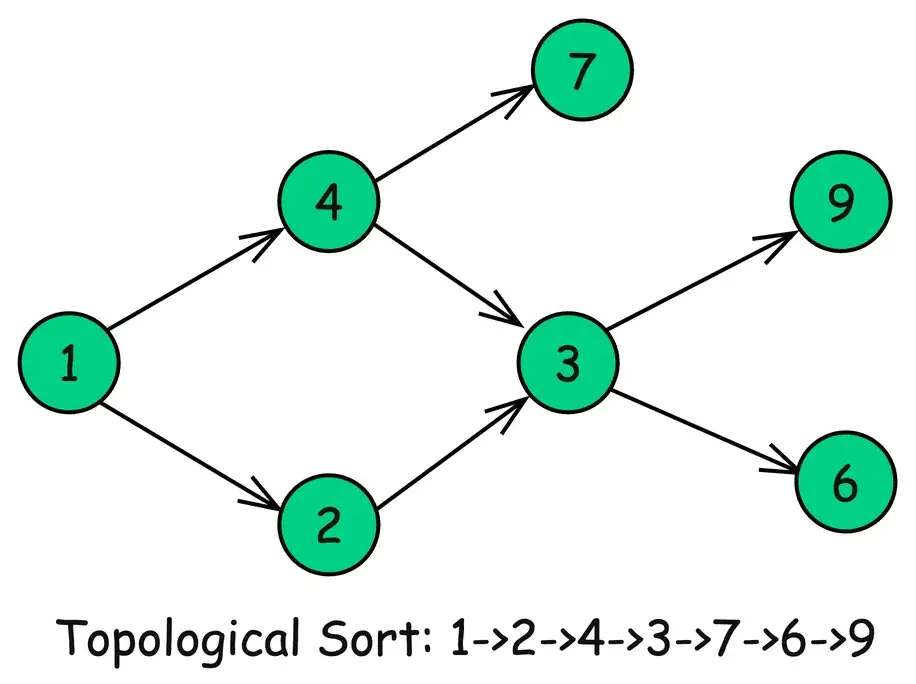
3. Топологическая сортировка

Топологическая сортировка

Алгоритм топологической сортировки используется для упорядочивания вершин ориентированного ациклического графа (DAG) в линейной последовательности таким образом, что для каждого направленного ребра u → v вершина u предшествует вершине v в порядке следования.

По сути, он упорядочивает узлы в последовательности, в которой все предварительные задачи предшествуют зависящим от них задачам.

Топологическая сортировка особенно полезна в таких сценариях, как:

• Определение порядка выполнения задач с учётом зависимостей (например, предварительных условий курса, систем сборки).
• Определение порядка установки программных пакетов, которые зависят друг от друга.
• Упорядочивание файлов или модулей таким образом, чтобы их можно было скомпилировать без ошибок из-за отсутствия зависимостей.

Существует два распространенных метода выполнения топологической сортировки:

1. Алгоритм, основанный на поиске в глубину (DFS):

def topological_sort_dfs(graph):
    visited = set()
    stack = []

    def dfs(vertex):
        visited.add(vertex)
        for neighbor in graph.get(vertex, []):
            if neighbor not in visited:
                dfs(neighbor)
        stack.append(vertex)

    for vertex in graph:
        if vertex not in visited:
            dfs(vertex)
    return stack[::-1]  # Переверните стопку, чтобы получить правильный порядок

Объяснение:

• Обход по методу DFS: посещайте каждый узел и рекурсивно исследуйте его соседей.
• Вставка после обхода: после посещения всех потомков узла добавьте его в стек.
• Результат: Переверните стек, чтобы получить топологический порядок.

2. Топологическая сортировка на основе BFS (алгоритм Кана):

from collections import deque

def topological_sort_kahn(graph):
    in_degree = {u: 0 for u in graph}
    for u in graph:
        for v in graph[u]:
            in_degree[v] = in_degree.get(v, 0) + 1

    queue = deque([u for u in in_degree if in_degree[u] == 0])
    topo_order = []

    while queue:
        u = queue.popleft()
        topo_order.append(u)
        for v in graph.get(u, []):
            in_degree[v] -= 1
            if in_degree[v] == 0:
                queue.append(v)

    if len(topo_order) == len(in_degree):
        return topo_order
    else:
        raise Exception("График имеет по крайней мере один цикл")

Объяснение:

• Вычислите степень вхождения: вычислите количество входящих рёбер для каждого узла.
• Инициализация очереди: начните с узлов, у которых нулевая степень вхождения.
• Узлы процесса:
  • Удалите узел из очереди, добавьте его в топологический порядок.
  • Уменьшают степень доступа к своим соседям.
  • Ставьте в очередь соседей, степень которых равна нулю.
• Обнаружение цикла: если топологический порядок не включает все узлы, граф содержит цикл.

Временная сложность: O(V + E), поскольку каждый узел и ребро обрабатываются ровно один раз.

Сложность по пространству: O(V) для хранения топологического порядка и вспомогательных структур данных, таких как множество посещённых вершин или массив степеней.

4. Поиск объединения

Поиск объединения

Объединение в группу — это структура данных, которая отслеживает набор элементов, разделённых на непересекающиеся (не имеющие общих элементов) подмножества.

Он поддерживает две основные операции:

1. Поиск (Find-Set): Определяет, к какому подмножеству относится конкретный элемент. Это можно использовать для проверки, находятся ли два элемента в одном подмножестве.
2. Объединение: объединяет два подмножества в одно, фактически соединяя два элемента.

Поиск обьединения особенно полезен в таких сценариях, как:

• Быстрая проверка, создает ли добавление ребра цикл в графике.
• Построение минимального остовного дерева путем соединения наименьших ребер без образования циклов.
• Определение того, находятся ли два узла в одном и том же подключенном компоненте.
• Группировка похожих элементов вместе.

Как работает Union Find:

Структура данных Union Find обычно состоит из:

1. Родительский массив (parent): Массив, в котором parent[i] хранится родительский элемент i. Изначально каждый элемент является своим собственным родителем.
2. Массив рангов (rank): Массив, который приблизительно соответствует глубине (или высоте) дерева, представляющего каждый набор. Используется для оптимизации объединений.

Операции:

• Найти(x):
  • Находит репрезентативный (корневой) набор, содержащий x.
  • Следует родительским указателям до тех пор, пока не достигнет узла, который является его собственным родительским узлом.
  • Сжатие пути используется для оптимизации временной сложности операции поиска за счёт того, что каждый узел на пути указывает непосредственно на корень, упрощая структуру.
• Объединение (x, y):
  • Объединяет наборы, содержащие x и y.
  • Найдите корни x и y, затем сделайте один корень родительским для другого.
  • Объединение по рангу используется для оптимизации, при которой корень меньшего дерева становится дочерним по отношению к корню большего дерева, чтобы дерево оставалось неглубоким.

Реализация:

class UnionFind:
    def __init__(self, size):
        self.parent = [i for i in range(size)]  # Изначально каждый узел является своим собственным родительским узлом
        self.rank = [0] * size  # Ранг (глубина) каждого дерева

    def find(self, x):
        if self.parent[x] != x:
            # Сжатие контура: сглаживание дерева
            self.parent[x] = self.find(self.parent[x])
        return self.parent[x]

    def union(self, x, y):
        # Найдите корни множеств, содержащих x и y
        root_x = self.find(x)
        root_y = self.find(y)

        if root_x == root_y:
            # Уже в том же наборе
            return

        # Объединение по рангу: прикрепите меньшее дерево к корню большего дерева
        if self.rank[root_x] < self.rank[root_y]:
            self.parent[root_x] = root_y
        elif self.rank[root_y] < self.rank[root_x]:
            self.parent[root_y] = root_x
        else:
            # Ранги равны; выберите один из них в качестве нового корня и увеличьте его ранг
            self.parent[root_y] = root_x
            self.rank[root_x] += 1

Временная сложность каждой операции:

• Поиск и объединение: амортизированная O(α(n)), где α(n) — обратная функция Аккермана, которая практически постоянна.
• Временная сложность: O(n), где n — количество элементов для хранения parent и rank массивов.

5. Обнаружение циклов

Обнаружение циклов

Обнаружение циклов заключается в определении того, содержит ли граф циклы — пути, в которых первая и последняя вершины совпадают, а рёбра не повторяются.

Другими словами, это последовательность вершин, начинающаяся и заканчивающаяся одной и той же вершиной, при этом каждая смежная пара соединена ребром.

Обнаружение цикла особенно важно в таких сценариях, как:

• Обнаружение заблокированных процессов в операционных системах для выявления циклических условий ожидания.
• Обеспечение отсутствия циклических зависимостей в системах управления пакетами или системах сборки.
• Понимание того, является ли граф деревом или циклическим графом.

Существуют различные подходы к обнаружению циклов в графах:

Обнаружение циклов в неориентированных графах с использованием DFS:

def has_cycle_undirected(graph):
    visited = set()

    def dfs(vertex, parent):
        visited.add(vertex)
        for neighbor in graph.get(vertex, []):
            if neighbor not in visited:
                if dfs(neighbor, vertex):
                    return True
            elif neighbor != parent:
                return True  # Обнаружен цикл
        return False

    for vertex in graph:
        if vertex not in visited:
            if dfs(vertex, None):
                return True
    return False

Объяснение:

• Обход DFS: запускайте DFS с непросмотренных узлов.
• Отслеживание родительского узла: отслеживайте родительский узел, чтобы избежать ложных срабатываний.
• Условие обнаружения цикла: если посещенный сосед не является родителем, то обнаруживается цикл.

Обнаружение циклов в ориентированных графах с использованием DFS:

def has_cycle_directed(graph):
    visited = set()
    recursion_stack = set()

    def dfs(vertex):
        visited.add(vertex)
        recursion_stack.add(vertex)
        for neighbor in graph.get(vertex, []):
            if neighbor not in visited:
                if dfs(neighbor):
                    return True
            elif neighbor in recursion_stack:
                return True  # Обнаружен цикл
        recursion_stack.remove(vertex)
        return False

    for vertex in graph:
        if vertex not in visited:
            if dfs(vertex):
                return True
    return False

Объяснение:

• Набор посещений и стек рекурсии:
  • visited отслеживает все посещенные узлы.
  • recursion_stack отслеживает узлы на текущем пути.
• Условие обнаружения цикла:
  • Если сосед находится в стеке рекурсии, обнаруживается цикл.

Обнаружение цикла с помощью Union-Find (неориентированные графы):

class UnionFind:
    def __init__(self):
        self.parent = {}

    def find(self, x):
        # Сжатие пути
        if self.parent.get(x, x) != x:
            self.parent[x] = self.find(self.parent[x])
        return self.parent.get(x, x)

    def union(self, x, y):
        root_x = self.find(x)
        root_y = self.find(y)
        if root_x == root_y:
            return False  # Обнаружен цикл
        self.parent[root_y] = root_x
        return True

def has_cycle_union_find(edges):
    uf = UnionFind()
    for u, v in edges:
        if not uf.union(u, v):
            return True
    return False

Объяснение:

• Инициализация: Создайте экземпляр UnionFind.
• Обработка ребер:
  • Для каждого ребра попытайтесь объединить вершины.
  • Если union возвращается False, обнаруживается цикл.

Временная сложность: O(V + E), так как каждый узел и ребро обрабатываются не более одного раза.

Сложность по памяти: O(V) для набора посещенных вершин и стека рекурсии в DFS.

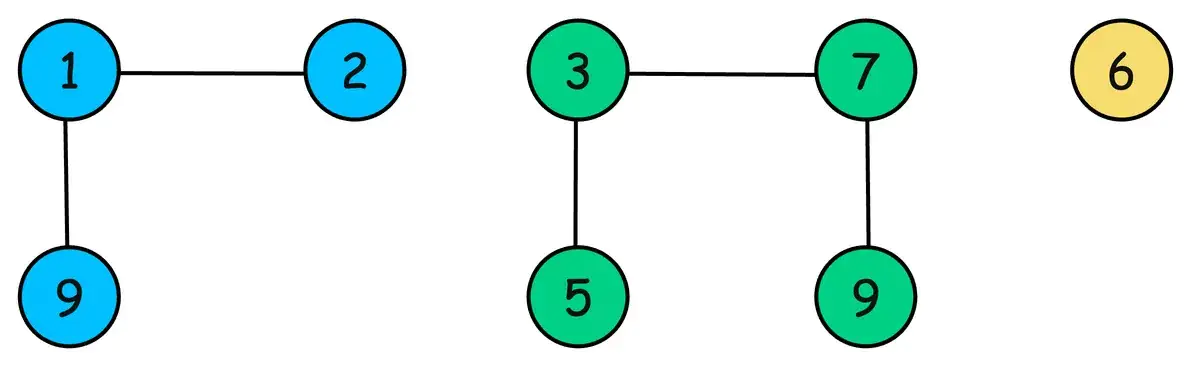
6. Связанные компоненты

В контексте неориентированных графов связный компонент — это набор вершин, в котором каждая вершина соединена по крайней мере с одной другой вершиной из того же набора с помощью некоторого пути.

По сути, это максимальная группа узлов, в которой каждый узел доступен из любого другого узла той же группы.

В ориентированных графах мы имеем дело с сильно связными компонентами (ССК), в которых существует ориентированный путь от каждой вершины к любой другой вершине в пределах одного компонента.

Как найти связанные компоненты:

Мы можем найти связные компоненты с помощью алгоритмов обхода графа, таких как поиск в глубину (DFS) или поиск в ширину (BFS).

Идея состоит в том, чтобы:

1. Инициализировать:
   • Создайте набор visited для отслеживания посещенных узлов.
   • Инициализируйте список components для хранения каждого подключенного компонента.
2. Обход:
   • Для каждого непросмотренного узла выполните DFS или BFS.
   • Отметьте все доступные узлы из этого узла как часть одного и того же компонента.
   • Добавьте компонент в список components.
3. Повторение:
   • Продолжайте процесс до тех пор, пока не будут посещены все узлы.

Реализация:

def connected_components(graph):
    visited = set()
    components = []

    def dfs(node, component):
        visited.add(node)
        component.append(node)
        for neighbor in graph.get(node, []):
            if neighbor not in visited:
                dfs(neighbor, component)

    for node in graph:
        if node not in visited:
            component = []
            dfs(node, component)
            components.append(component)

    return components

Объяснение:

• Посещаемый набор: отслеживает посещенные узлы, чтобы предотвратить повторный переход.
• Функция DFS:
  • Рекурсивно исследует всех соседей узла.
  • Добавляет каждый посещенный узел к текущему component.
• Основной цикл:
  • Выполняет итерации по всем узлам графика.
  • Для непросмотренных узлов инициирует DFS и собирает подключенный компонент.

Временная сложность: O(V + E), поскольку каждый узел и ребро посещаются ровно один раз.

Сложность по памяти: O(V) из-за набора visited и стека рекурсии (в DFS) или очереди (в BFS).

Сильно связанные компоненты в ориентированных графах:

Чтобы найти сильно связные компоненты в ориентированном графе, вы можете использовать такие алгоритмы, как алгоритм Косараджу или алгоритм Тарджана.

Шаги алгоритма Косараджу:

1. Первый проход: Выполните DFS на исходном графе, чтобы вычислить время завершения работы каждого узла.
2. Транспонировать граф: изменить направление всех ребер на обратное.
3. Второй проход: Выполните DFS на транспонированном графе в порядке убывания времени завершения первого прохода.
4. Результат: каждый обход DFS во втором проходе идентифицирует сильно связанный компонент.

7. Двудольные графы

Двудольные графы

Двудольный граф — это тип графа, вершины которого могут быть разделены на два непересекающихся и независимых множества, обычно обозначаемых как U и V, так что каждое ребро соединяет вершину из U с вершиной из V.

Другими словами, никакое ребро не соединяет вершины в пределах одного набора.

Представьте себе две группы людей на вечеринке: одну группу интервьюеров, а другую — кандидатов. Вершины представляют собой интервью между интервьюером и кандидатом. Поскольку ни один интервьюер не берёт интервью у другого интервьюера, а ни один кандидат не берёт интервью у другого кандидата, граф естественным образом делится на два множества, становясь двудольным.

Свойства двудольных графов:

• Двудольный граф: граф является двудольным тогда и только тогда, когда его можно раскрасить двумя цветами так, чтобы никакие две смежные вершины не были одного цвета.
• Нет циклов нечётной длины: двудольные графы не содержат циклов нечётной длины.

Как проверить, является ли граф двудольным:

Мы можем определить, является ли граф двудольным, попытавшись раскрасить его двумя цветами, не присваивая один и тот же цвет смежным вершинам. Если это удалось, то граф является двудольным.

Это можно сделать с помощью:

• Поиск в ширину (BFS): назначайте цвета уровень за уровнем.
• Поиск в глубину (DFS): Рекурсивно назначайте цвета.

Реализация с использованием BFS

from collections import deque

def is_bipartite(graph):
    color = {}
    for node in graph:
        if node not in color:
            queue = deque([node])
            color[node] = 0  # Назначьте первый цвет
            while queue:
                current = queue.popleft()
                for neighbor in graph[current]:
                    if neighbor not in color:
                        color[neighbor] = 1 - color[current]  # Назначьте противоположный цвет
                        queue.append(neighbor)
                    elif color[neighbor] == color[current]:
                        return False  # Соседние узлы имеют одинаковый цвет
    return True

Объяснение:

• Инициализация: создайте словарь color для хранения цвета, присвоенного каждому узлу.
• Обход BFS: Для каждого неокрашенного узла запустите BFS.
  • Назначьте начальному узлу цвет (0 или 1).
  • Для каждого соседа:
    • Если они не окрашены, присвоите им противоположный цвет и поставьте в очередь.
    • Если он уже окрашен и имеет тот же цвет, что и текущий узел, то граф не является двудольным.
• Результат: Если обход завершается без конфликтов, граф является двудольным.

Временная сложность: O(V + E), поскольку каждый узел и ребро посещаются ровно один раз.

Сложность по памяти: O(V) из-за набора color и стека рекурсии (в DFS) или очереди (в BFS).

8. Заливка флудом

Заливка — это алгоритм, который определяет и изменяет область, связанную с заданным узлом в многомерном массиве.

Начиная с начальной точки, он находит или заполняет (или перекрашивает) все связанные пиксели или ячейки с одинаковым цветом или значением.

Как работает заливка флудом:

1. Начальная точка: начните с начального пикселя (начальных координат).
2. Проверьте цвет: если цвет текущего пикселя совпадает с целевым цветом (который нужно заменить), продолжайте.
3. Замените цвет: измените цвет текущего пикселя на новый.
4. Рекурсивный визит к соседям:
   • Перейдите к соседним пикселям (вверх, вниз, влево, вправо или по диагонали, в зависимости от реализации).
   • Повторите процесс для каждого соседа, который соответствует целевому цвету.
5. Завершение: Алгоритм завершается, когда все связанные пиксели целевого цвета обработаны.

Реализация

Рекурсивное заполнение потоком:

def flood_fill_recursive(image, sr, sc, new_color):
    rows, cols = len(image), len(image[0])
    color_to_replace = image[sr][sc]
    if color_to_replace == new_color:
        return image

    def dfs(r, c):
        if (0 <= r < rows and 0 <= c < cols and image[r][c] == color_to_replace):
            image[r][c] = new_color
            # Исследуйте соседей: up, down, left, right
            dfs(r + 1, c)  # Вниз
            dfs(r - 1, c)  # Вверх
            dfs(r, c + 1)  # Влево
            dfs(r, c - 1)  # Вправо

    dfs(sr, sc)
    return image

Объяснение:

• Базовый случай: Если заменяемый цвет совпадает с новым цветом, верните изображение без изменений.
• Функция DFS:
  • Проверяет границы и соответствует ли текущий пиксель цвету, который нужно заменить.
  • Изменяет цвет текущего пикселя.
  • Рекурсивно вызывает себя на соседних пикселях.

Итеративное заполнение потоком:

from collections import deque

def flood_fill_iterative(image, sr, sc, new_color):
    rows, cols = len(image), len(image[0])
    color_to_replace = image[sr][sc]
    if color_to_replace == new_color:
        return image

    queue = deque()
    queue.append((sr, sc))
    image[sr][sc] = new_color

    while queue:
        r, c = queue.popleft()
        for dr, dc in [(-1, 0), (1, 0), (0, -1), (0, 1)]:  # Направления: up, down, left, right
            nr, nc = r + dr, c + dc
            if (0 <= nr < rows and 0 <= nc < cols and image[nr][nc] == color_to_replace):
                image[nr][nc] = new_color
                queue.append((nr, nc))

    return image

Объяснение:

• Инициализация:
  • Используйте a deque в качестве очереди для управления пикселями для обработки.
  • Начните с постановки в очередь начального пикселя.
• Цикл обработки:
  • Удаление пикселя из очереди.
  • Для каждого направления (вверх, вниз, влево, вправо) проверьте, нужно ли заполнить соседнюю ячейку.
  • Если да, измените его цвет и поставьте в очередь.
• Завершение:
  • Цикл заканчивается, когда больше не остается пикселей для обработки.

Временная сложность: O(N), где N — количество пикселей в области, которую нужно заполнить. Каждый пиксель посещается не более одного раза.

Пространственная сложность:

• Рекурсивная реализация: O(N) из-за стека вызовов в рекурсии.
• Итеративная реализация: O(N), если для управления пикселями используется очередь или стек.

9. Минимальное связующее дерево

Минимальное связующее дерево (MST)

MST — это подмножество ребер связного, неориентированного, взвешенного графа, который соединяет все вершины вместе без каких-либо циклов и с минимально возможным общим весом ребер.

Проще говоря, это самый дешёвый способ соединить все узлы в сети без каких-либо петель.

Ключевые алгоритмы поиска MST:

1. Алгоритм Крускала:

• Построение MST путём последовательного добавления рёбер, начиная с самых маленьких.
• Использует структуру данных Union Find для обнаружения циклов.

Реализация:

class UnionFind:
    def __init__(self, size):
        self.parent = [i for i in range(size)]
        self.rank = [0] * size

    def find(self, x):
        if self.parent[x] != x:
            # Сжатие пути
            self.parent[x] = self.find(self.parent[x])
        return self.parent[x]

    def union(self, x, y):
        root_x = self.find(x)
        root_y = self.find(y)
        if root_x == root_y:
            return False  # Обнаружен цикл
        # Объединение по рангу
        if self.rank[root_x] < self.rank[root_y]:
            self.parent[root_x] = root_y
        elif self.rank[root_y] < self.rank[root_x]:
            self.parent[root_y] = root_x
        else:
            self.parent[root_y] = root_x
            self.rank[root_x] += 1
        return True

def kruskal_mst(num_nodes, edges):
    # edges - это список кортежей: (weight, node_u, node_v)
    uf = UnionFind(num_nodes)
    mst = []
    total_weight = 0

    # Сортировка ребер по весу
    edges.sort(key=lambda x: x[0])

    for weight, u, v in edges:
        if uf.union(u, v):
            mst.append((u, v, weight))
            total_weight += weight
            print(f"Edge добавлен: ({u}, {v}) with weight {weight}")
        else:
            print(f"Edge ({u}, {v}) с весом {weight} создает цикл и пропускается.")

    print(f"Общий вес MST: {total_weight}")
    return mst

Объяснение:

• Класс UnionFind:
  • Управляет непересекающимися наборами для эффективного обнаружения циклов.
• Сортировка по краям:
  • Ребра сортируются по весу, чтобы в первую очередь учитывать наименьшие ребра.
• Основной цикл:
  • Выполняет итерацию по отсортированным ребрам.
  • Пытается объединить множества, содержащие вершины ребра.
  • Если объединение выполнено успешно, ребро добавляется к MST.
  • Если это приведет к созданию цикла, ребро пропускается.

Временная сложность: O(E log E), так как сортировка рёбер занимает O(E log E), а операции объединения и поиска выполняются практически за постоянное время

Сложность по пространству: O(V + E), O(V) для хранения массивов родительских вершин и рангов в алгоритме объединения и O(E) для хранения рёбер.

2. Алгоритм Прима:

• Начинает с произвольного узла и наращивает MST, добавляя самый дешёвый путь из дерева к новой вершине.

import heapq

def prim_mst(graph, start=0):
    num_nodes = len(graph)
    visited = [False] * num_nodes
    min_heap = [(0, start, -1)]  # (weight, current_node, parent_node)
    mst = []
    total_weight = 0

    while min_heap and len(mst) < num_nodes - 1:
        weight, u, parent = heapq.heappop(min_heap)
        if not visited[u]:
            visited[u] = True
            if parent != -1:
                mst.append((parent, u, weight))
                total_weight += weight
                print(f"Edge добавлен: ({parent}, {u}) with weight {weight}")

            for v, w in graph[u]:
                if not visited[v]:
                    heapq.heappush(min_heap, (w, v, u))

    if len(mst) != num_nodes - 1:
        print("График не подключен.")
        return None

    print(f"Общий вес MST: {total_weight}")
    return mst

Объяснение:

• Инициализация:
  • visited массив отслеживает посещенные узлы.
  • min_heap является приоритетной очередью, инициализированной начальным узлом.
• Основной цикл:
  • Пока куча не пуста, а MST неполон:
    • Выделите ребро с минимальным весом.
    • Если узел не был посещен:
      • Отметьте его как посещенное.
      • Добавьте ребро в MST (если это не начальный узел).
      • Добавьте все ребра из этого узла в кучу.
• Завершение:
  • Алгоритм завершается, когда все узлы включены в MST.
  • Проверяет, охватывает ли MST все узлы (граф связан).

Временная сложность: O(E log V) при использовании очереди с приоритетом (минимальная куча).

Сложность по памяти: O(V) для очереди с приоритетом и используемых массивов.

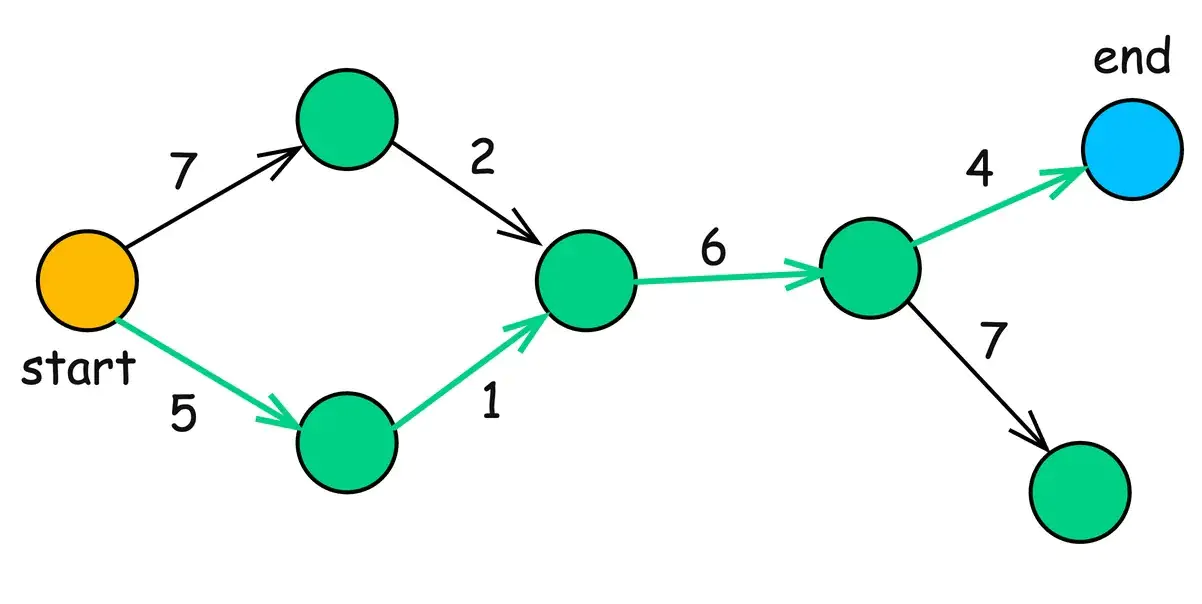
10. Кратчайший путь

Кратчайший путь

Задача о кратчайшем пути заключается в поиске пути между двумя вершинами (узлами) графа, сумма весов составляющих его рёбер которого минимальна.

Проще говоря, речь идёт о поиске наиболее эффективного маршрута от начальной точки к конечному пункту назначения в сети.

Ключевые алгоритмы поиска кратчайших путей:

1. Алгоритм Дейкстры:

• Находит кратчайшие пути от одной исходной вершины ко всем остальным вершинам в графе с неотрицательными весами рёбер.
• Это жадный алгоритм, использующий очередь с приоритетами (минимальную кучу).

import heapq

def dijkstra(graph, start):
    # график: список смежностей, где graph[u] = [(v, weight), ...]
    distances = {vertex: float('inf') для вершины в графе}
    distances[start] = 0
    priority_queue = [(0, start)]
    while priority_queue:
        current_distance, current_vertex = heapq.heappop(priority_queue)
        # Пропустите, если мы уже нашли лучший путь
        if current_distance > distances[current_vertex]:
            continue
        for neighbor, weight in graph[current_vertex]:
            distance = current_distance + weight
            # Если найден более короткий путь к соседу
            if distance < distances[neighbor]:
                distances[neighbor] = distance
                heapq.heappush(priority_queue, (distance, neighbor))
    return distances

Объяснение:

• Инициализация:
  • distances словарь хранит кратчайшее известное расстояние до каждой вершины.
  • priority_queue это минимальная куча, хранящая кортежи (distance, vertex).
• Основной цикл:
  • Выберите вершину с наименьшим известным расстоянием.
  • Для каждого соседа вычислите новое расстояние.
  • Если новое расстояние короче, обновите и перенесите в кучу.
• Результат:
  • Возвращает кратчайшее расстояние от начальной вершины до всех остальных вершин.

Временная сложность: O(V + E log V) при использовании минимальной кучи (очереди с приоритетом).

Сложность по пространству: O(V) для хранения расстояний и очереди с приоритетом.

2. Алгоритм Беллмана-Форда:

• Вычисляет кратчайшие пути от одной исходной вершины ко всем остальным вершинам, даже если в графе есть отрицательные веса рёбер.
• Он может обнаруживать негативные циклы.

def bellman_ford(graph, start):
    # график: список ребер [(u, v, weight), ...]
    num_vertices = len({u для ребра в графе для u в edge[:2]})
    distances = {vertex: float('inf') для ребра в графе, для вершины в edge[:2]}
    distances[start] = 0

    # Несколько раз расслабьте края
    for _ in range(num_vertices - 1):
        for u, v, weight in graph:
            if distances[u] + weight < distances[v]:
                distances[v] = distances[u] + weight

    # Проверьте наличие циклов с отрицательным весом
    for u, v, weight in graph:
        if distances[u] + weight < distances[v]:
            raise Exception("График содержит цикл с отрицательным весом")

    return distances

Объяснение:

• Инициализация: distances в словаре хранится кратчайшее известное расстояние до каждой вершины.
• Основной цикл: Повторяйте num_vertices - 1 раз, расслабляя все мышцы.
• Проверка отрицательного цикла: окончательный проход для проверки улучшений указывает на отрицательный цикл.
• Результат: возвращает кратчайшие расстояния от начальной вершины до всех остальных вершин.

Временная сложность: O (V * E)

Сложность пространства: O (V) для хранения расстояний.

3. Поиск по ширине (BFS):

• Применимо для невзвешенных графов или графов, в которых все рёбра имеют одинаковый вес.
• Находит кратчайший путь, исследуя соседние узлы уровень за уровнем.

from collections import deque

def bfs_shortest_path(graph, start, target):
    visited = set()
    queue = deque([(start, [start])])  # Each element is a tuple (node, path_to_node)
    visited.add(start)

    while queue:
        current_node, path = queue.popleft()

        if current_node == target:
            return path  # Найден кратчайший путь

        for neighbor in graph[current_node]:
            if neighbor not in visited:
                visited.add(neighbor)
                queue.append((neighbor, path + [neighbor]))

    return None  # Путь не найден

4. Алгоритм A * (A-Star):

• Используется для графиков, где у вас есть эвристическая оценка расстояния до цели.
• Обычно используется для поиска пути и обхода графов, особенно в играх и приложениях с искусственным интеллектом.

Как это работает:

• A* сочетает в себе функции алгоритма Дейкстры и жадного поиска в первую очередь.
• Он выбирает путь, который сводит к минимуму f(n) = g(n) + h(n), где:
  • g(n)это фактическая стоимость перехода от начального узла к текущему узлуn.
  • h(n) — эвристическая оценочная стоимость от n до цели.

Реализация:

import heapq

def a_star(graph, start, goal, heuristic):
    open_set = []
    heapq.heappush(open_set, (0 + heuristic(start, goal), 0, start, [start]))  # (f_score, g_score, node, path)
    closed_set = set()

    while open_set:
        f_score, g_score, current_node, path = heapq.heappop(open_set)

        if current_node == goal:
            return path  # Найден кратчайший путь

        if current_node in closed_set:
            continue
        closed_set.add(current_node)

        for neighbor, weight in graph[current_node]:
            if neighbor in closed_set:
                continue
            tentative_g_score = g_score + weight
            tentative_f_score = tentative_g_score + heuristic(neighbor, goal)
            heapq.heappush(open_set, (tentative_f_score, tentative_g_score, neighbor, path + [neighbor]))

    return None  # Путь не найден

Временная сложность:

• В худшем случае: O(b^d), где b — коэффициент ветвления (среднее количество потомков в каждом состоянии), а d — глубина решения.
• В лучшем случае: O(d), когда эвристическая функция идеальна и ведёт непосредственно к цели.

Сложность по памяти: O(b^d), так как необходимо хранить все сгенерированные узлы в памяти.

5. Алгоритм Флойда-Уорсхолла:

• Вычисляет кратчайший путь между всеми парами вершин.
• Подходит для плотных графов с меньшим числом вершин.
• Алгоритм итеративно обновляет кратчайшие пути между всеми парами вершин, рассматривая все возможные промежуточные вершины.

Реализация:

def floyd_warshall(graph):
    # Инициализируйте матрицы distance и next_node
    nodes = list(graph.keys())
    dist = {u: {v: float('inf') for v in nodes} for u in nodes}
    next_node = {u: {v: None for v in nodes} for u in nodes}

    # Инициализируйте расстояния на основе прямых ребер
    for u in nodes:
        dist[u][u] = 0
        for v, weight in graph[u]:
            dist[u][v] = weight
            next_node[u][v] = v

    # Алгоритм Флойда-Уоршалла
    for k in nodes:
        for i in nodes:
            for j in nodes:
                if dist[i][k] + dist[k][j] < dist[i][j]:
                    dist[i][j] = dist[i][k] + dist[k][j]
                    next_node[i][j] = next_node[i][k]

    # Проверьте наличие отрицательных циклов
    for u in nodes:
        if dist[u][u] < 0:
            raise Exception("График содержит цикл с отрицательным весом")

    return dist, next_node

Временная сложность: O (V ^ 3)

Сложность по памяти: O(V^2) для хранения массива расстояний.

Надеюсь, вам понравилось читать эту статью.

Если вы нашли эту статью полезной, поставьте лайк ❤️.

Если у вас есть какие-либо вопросы или предложения, оставьте комментарий.

Редактор: AndreyEx