Термин «Наименьшее общее кратное» (LCM) относится к наименьшему числу, которое делится на все заданные числа в наборе целых чисел в математике. В C ++ доступно множество методов вычисления LCM из двух чисел, таких как использование «условия if», «цикла while» или метода GCD (наибольшего общего делителя), среди прочих.
Что такое LCM из двух чисел в Python?
LCM, также известная как наименьшее общее кратное, представляет собой математическую концепцию, используемую для нахождения наименьшего числа (обозначаемого как LCM (a, b) или lcm (a, b)), которое делится на оба заданных числа (n1 и n2). Она представляет собой общее кратное, которое существует в обоих числах.
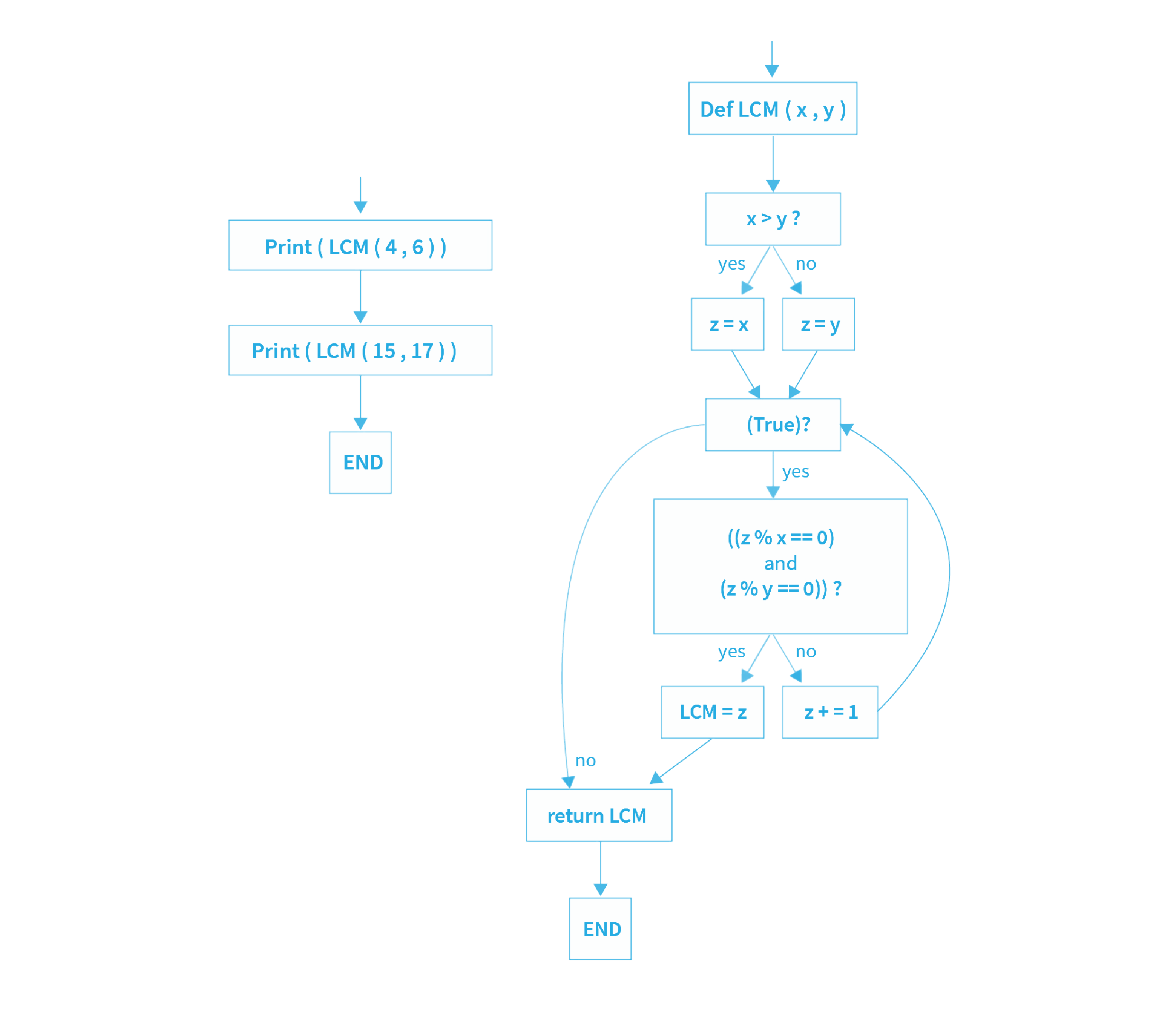
Блок-схема LCM из двух чисел на Python
Алгоритм программы на Python для нахождения LCM из двух чисел:
- Шаг 1: Примите два входных сигнала от пользователя n1 и n2
- Шаг 2: Запишите наименьшее общее кратное n1 и n2 в переменную max.
- Шаг 3: Проверьте, делится ли переменная max на n1 и n2, и выведите max как LCM из двух чисел.
- Шаг 4: В противном случае максимальное значение обновляется на 1 на каждой итерации, и переходите к шагу 3, чтобы проверить делимость переменной max.
- Шаг 5: Завершите работу программы
Методы программы на Python для нахождения LCM из двух чисел
В Python существует несколько методов нахождения LCM (наименьшего общего кратного) из двух чисел. Вот несколько часто используемых подходов:
С использованием метода GCD (наибольшего общего делителя):
Import математического модуля math.
- Используйте функцию math.gcd(), чтобы найти НОД двух чисел.
- Вычислите LCM, используя формулу: LCM(a, b) = (a * b) / GCD(a, b).
Реализация кода:
import math
def lcm(a, b):
gcd = math.gcd(a, b)
lcm = (a * b) // gcd
return lcm
Использование цикла:
- Начните с большего из двух чисел.
- Используйте цикл для увеличения на большее число, пока не будет найдено общее кратное.
- Проверьте, делится ли текущее число на оба числа.
- Возвращает первое найденное число, удовлетворяющее этому условию.
Реализация кода:
def lcm(a, b):
max_num = max(a, b)
while True:
if max_num % a == 0 and max_num % b == 0:
return max_num
max_num += 1
Используя формулу LCM:
Calculate the product of the two numbers. Divide the product by their GCD to get the LCM.
Реализация кода:
def lcm(a, b):
lcm = (a * b) // math.gcd(a, b)
return lcm
Эти методы можно использовать для нахождения LCM из любых двух заданных чисел на Python. Выберите метод, соответствующий вашим требованиям и предпочтениям.
Заключение
В заключение, нахождение LCM (наименьшего общего кратного) двух чисел является обычной математической операцией, и Python предоставляет различные методы для выполнения этой задачи. Используя GCD (наибольший общий делитель), цикл или формулу LCM, вы можете эффективно рассчитать LCM. Эти методы обеспечивают гибкость, позволяя вам выбрать подход, который наилучшим образом соответствует вашим конкретным требованиям.
Часто задаваемые вопросы, связанные с программой на Python для поиска LCM из двух чисел
Вот несколько часто задаваемых вопросов, связанных с программой на Python для поиска LCM из двух чисел:
Вопрос 1. Как я могу найти LCM из двух чисел на Python?
Вы можете использовать такие методы, как метод GCD, метод цикла или формулу LCM, чтобы найти LCM из двух чисел на Python.
Вопрос 2. Что такое GCD и как он связан с LCM?
НОД (наибольший общий делитель) — это наибольшее положительное целое число, которое делит оба заданных числа без остатка. НОД вычисляется с использованием НОД в некоторых методах, таких как формула НОД.
Вопрос 3. Могу ли я использовать функцию LCM из математической библиотеки на Python?
Математическая библиотека Python не имеет встроенной функции LCM. Однако вы можете использовать функцию math.gcd() из математической библиотеки, чтобы помочь вычислить LCM.
Вопрос 4. Существуют ли какие-либо библиотеки Python, специально разработанные для вычислений LCM?
Хотя в Python нет специальных библиотек для вычислений LCM, вы можете создавать свои собственные повторно используемые функции или импортировать математическую библиотеку для вычислений GCD, чтобы эффективно находить LCM.