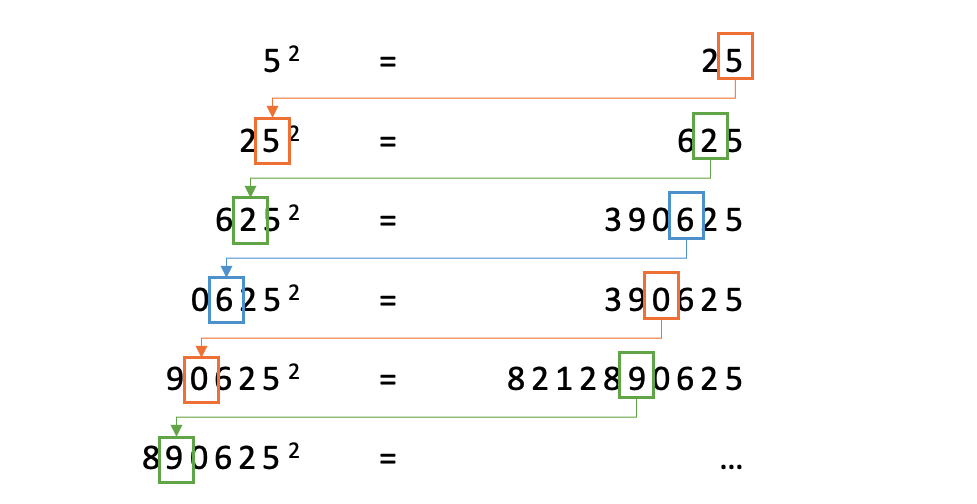Представьте число, обладающее необычной характеристикой: его квадрат заканчивается теми же цифрами, что и само число. Эти числа, известные как автоморфные числа, обладают замечательной способностью сохранять свою идентичность даже после математического преобразования. Они образуют увлекательное царство, где цифры заключают в себе их собственное зеркальное отражение, создавая интригующую головоломку, ожидающую разгадки.
В этой статье мы отправляемся в путешествие в очаровательный мир автоморфных чисел. Мы изучим их определение, свойства и раскроем основополагающие принципы, которые делают их уникальными. От их древнего происхождения до современных применений мы углубимся в различные аспекты автоморфных чисел и станем свидетелями увлекательного взаимодействия математики и теории чисел.
Что такое автоморфные числа?
Чтобы понять автоморфные числа, мы должны сначала усвоить их фундаментальное определение. Автоморфное число — это ненулевое положительное целое число, которое при возведении в квадрат дает результат, в котором его исходное число отображается в виде конечных цифр. Другими словами, автоморфное число «отражает» себя в пределах своего квадрата. Например, давайте рассмотрим автоморфное число 5. Когда мы возводим его в квадрат, результат равен 25, а в конце появляется цифра 5.
Свойства и характеристики:
Автоморфные числа обладают набором уникальных свойств, которые отличают их от других чисел. Вот некоторые ключевые характеристики автоморфных чисел:
- Саморефлексия: Как упоминалось ранее, определяющей чертой автоморфных чисел является их способность сохранять свою идентичность в пределах своего квадрата. Это самоотражающее свойство придает им ощущение симметрии и добавляет элемент интриги в их природу.
- Конечные цифры: Автоморфные числа в первую очередь идентифицируются по их конечным (или конечным) цифрам. Эти цифры имеют решающее значение для определения того, квалифицируется ли число как автоморфное, поскольку они должны совпадать с соответствующими цифрами в конце его квадрата.
- Расположение цифр: Положение автоморфных цифр внутри квадрата зависит от количества цифр в исходном числе. Например, однозначное автоморфное число будет иметь свою цифру в единицах измерения в своем квадрате, в то время как двузначное автоморфное число будет иметь свои цифры в единицах измерения и десятках, и так далее.
Примеры автоморфных чисел:
Давайте рассмотрим несколько примеров, чтобы проиллюстрировать концепцию автоморфных чисел:
Число 5 является автоморфным числом, поскольку его квадрат, 25, заканчивается цифрой 5.
Аналогично, число 76 является автоморфным числом, поскольку его квадрат, 5776, заканчивается теми же двумя цифрами.
Число 376 не является автоморфным числом, поскольку его квадрат, 141 376, не заканчивается исходными цифрами.
Определение того, является ли число Автоморфным числом или нет
Вам дано число N, и ваша задача состоит в том, чтобы определить, является ли это автоморфным числом. В нашем введении мы обсудили, что такое автоморфное число, и привели пример. Теперь давайте быстро обсудим, как мы можем подойти к этой проблеме.
Подход 1: определение того, является ли число автоморфным числом или нет
- Следите за квадратом данного числа.
- Выполняйте цикл до тех пор, пока N не станет равным 0, потому что нам нужно сопоставить все цифры с их квадратами.
- Проверьте, является ли (n%10 == sq%10), то есть является ли последняя цифра числа последней цифрой квадрата, истинным. Если не равно, верните false .
- В противном случае уменьшите число и квадрат, т.е. n = n/10 и sq = sq/10;
- Если все цифры совпадают, верните true.
Реализация кода
Код на C ++:- https://ideone.com/VakVKL
Код на Python:- https://ideone.com/wu54gB
Код Java:- https://ideone.com/denhm4
Вывод:
Automorphic
Временная сложность: O (log10N)
Подход 2: определение того, является ли число автоморфным числом или нет
- Проверьте, является ли число отрицательным, затем сделайте его положительным.
- Сохраните квадрат числа.
- Найдите количество цифр числа, чтобы вы могли найти количество цифр последнего числа в квадрате числа, равное числу; обратите внимание, что это не означает, что если количество последнего числа в квадрате равно числу, они будут равны.
- После подсчета цифр числа выполните: квадратное число в% степени (10, количество)
- Наконец, проверьте, равен ли последний квадрат числа самому числу.
Реализация кода
Код на C ++:- https://ideone.com/tFCssX
Код на Python:- https://ideone.com/xiFK9B
Код Java:- https://ideone.com/ZZlJVX
Вывод:
Not Automorphic
Временная сложность: O (log10N)
Применение и значение:
Автоморфные числа, хотя и интересны сами по себе, также находят практическое применение в различных областях. Некоторые области, где автоморфные числа оказались полезными, включают:
- Математика и теория чисел: Изучение автоморфных чисел углубляет наше понимание теории чисел и служит богатым источником математических исследований. Они дают представление о числовых шаблонах, последовательностях и взаимосвязях между числами.
- Криптография: Автоморфные числа могут играть определенную роль в определенных криптографических алгоритмах. Их уникальные свойства могут быть использованы для улучшения методов шифрования и обеспечения безопасной связи.
- Цифровая безопасность: Автоморфные числа способствуют разработке безопасных систем и протоколов, добавляя дополнительный уровень сложности и непредсказуемости криптографическим алгоритмам.
Заключение
В заключение, исследование автоморфных чисел отправляет нас в увлекательное путешествие по царству самоотражающихся цифр. Эти числа, с их способностью сохранять свою идентичность в пределах своих квадратов, позволяют заглянуть в сложные закономерности и симметрии, которые лежат в мире математики. Начиная с их определения и свойств и заканчивая приложениями в криптографии и цифровой безопасности, автоморфные числа доказали свою интеллектуальную стимулирующую и практическую значимость.
Разгадывая секреты автоморфных чисел, мы углубляем наше понимание теории чисел, раскрывая скрытые связи и проливая свет на увлекательное взаимодействие между цифрами и их квадратами. Изучение автоморфных чисел не только обогащает математические знания, но и способствует разработке защищенных систем и криптографических алгоритмов, укрепляя цифровую безопасность во все более взаимосвязанном мире.
Завершая это исследование, мы приглашаем вас ощутить красоту автоморфных чисел и продолжить свое путешествие по обширному ландшафту математики. Царство чисел наполнено тайнами, которые еще предстоит разгадать, и автоморфные числа служат напоминанием о захватывающей и постоянно развивающейся природе математических открытий.
Часто задаваемые вопросы (FAQs):
Вопрос 1: Ограничены ли автоморфные числа определенными цифрами?
Нет, автоморфные числа могут состоять из любых целых положительных цифр. Они могут варьироваться от однозначных до многозначных чисел, в зависимости от их свойств.
Вопрос 2: Существует ли бесконечно много автоморфных чисел?
Да, автоморфных чисел бесконечно много. Существование автоморфных чисел может быть доказано с помощью математических рассуждений и исследований.
Вопрос 3: Могут ли автоморфные числа содержать более одной цифры в конце своих квадратов?
Да, автоморфные числа могут содержать несколько цифр в конце своих квадратов. Количество цифр в конце квадрата зависит от количества цифр в исходном числе.
Вопрос 4: Могут ли автоморфные числа быть отрицательными или дробными?
Нет, автоморфные числа определяются как ненулевые положительные целые числа. Отрицательные числа и дроби не попадают в категорию автоморфных чисел.
Вопрос 5: Какое значение автоморфные числа имеют в криптографии?
Автоморфные числа могут использоваться в криптографических алгоритмах для улучшения методов шифрования и обеспечения безопасной связи. Их уникальные свойства усложняют и вносят вклад в общую безопасность криптографических систем.
Вопрос 6: Можно ли использовать автоморфные числа в других разделах математики?
Абсолютно! Автоморфные числа находят применение в различных математических областях, включая теорию чисел, последовательности и шаблоны. Они дают ценную информацию о базовых принципах и взаимосвязях в области математики.