Алгоритм топологической сортировки

Алгоритм топологической сортировки работает с DAG (прямой ациклический граф). Смысл топологической сортировки в том, что если какой-либо узел указывает на другой узел, то после него будет идти узел, указывающий на другой узел. Таким образом, в этом случае, если у нас есть циклический граф, мы не можем предсказать, какой узел после какого узла. Вот почему алгоритм топологической сортировки работает только с ациклическим графом, а не с циклическим графом.

Каждый граф имеет более одной топологической последовательности сортировки, поскольку она зависит от степени вхождения ребер узлов. Первый начальный узел, который мы выбираем с числом узлов в степени, равен 0.

Давайте разберемся с алгоритмом топологической сортировки на примере.

 

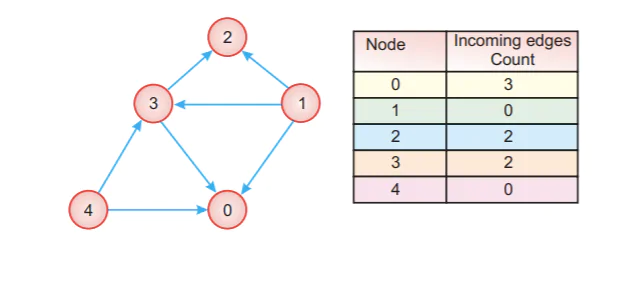
Шаг 1: мы вставляем те узлы, количество входящих ребер которых равно 0. Таким образом, эти узлы являются узлами 1 и 4.

 

Шаг 2:

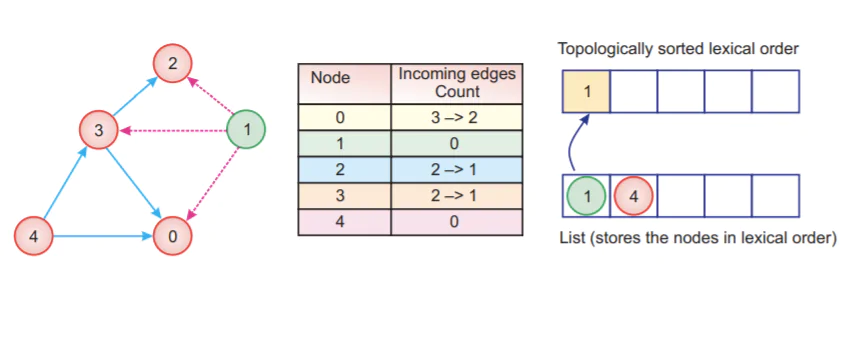
а. Начнем с узла 1. Мы можем выбрать любой узел между узлами 1 и 4.

б. Мы уменьшаем каждое ребро узла на 1, которое связано с узлом 1. Мы уменьшаем ребро узлов (0, 2 и 3).

в. Мы перемещаем узел 1 из списка в топологически отсортированный список, как показано ниже.

 

Шаг 3:

а. Теперь мы исходим из списка, который является Node 4.

б. Мы уменьшаем все исходящие ребра узлов, соединенных с узлом 4, которые являются узлами (0 и 3).

в. Теперь узел 3 не имеет входящих ребер, поэтому мы помещаем его в список, а узел 4 переходит в топологически отсортированный список.

 

Шаг 4:

а. Теперь мы исходим из списка, который является узлом 3.

б. Мы уменьшаем все исходящие ребра узлов, соединенных с узлом 3, которые являются узлами (0 и 2).

в. Теперь узлы 0 и 2 не имеют входящих ребер, поэтому мы помещаем их в список, а узел 3 переходит в топологически отсортированный список.

 

Шаг 5:

а. Теперь мы исходим из списка, который является Node 0.

б. Поскольку исходящих ребер из Node 0 нет, мы просто добавляем их в список топологической сортировки.

 

Шаг 6:

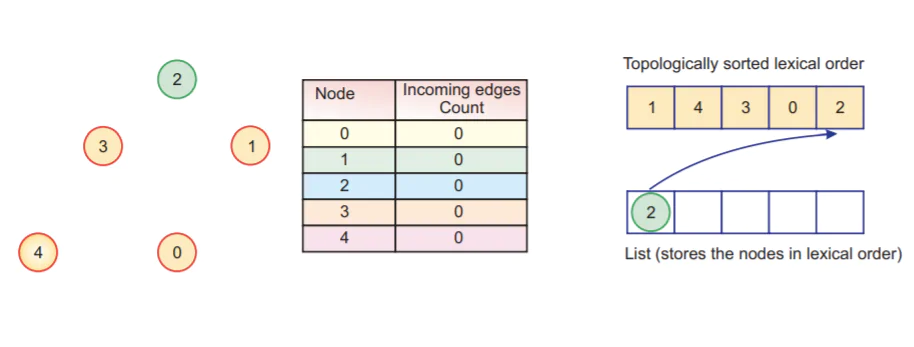
а. Теперь мы исходим из списка, который является узлом 2.

б. Поскольку исходящих ребер из узла 2 нет, мы просто добавляем их в список топологической сортировки.

 

Шаг 7:

Наконец, мы отсортировали список здесь.

 

Алгоритм топологической сортировки

Ниже приведены шаги алгоритма топологической сортировки, которым мы должны следовать.

Шаг 0: Рассчитайте степень вхождения каждого узла графа.

Шаг 1: Сначала нам нужно найти узел, у которого входящие ребра равны нулю.

Шаг 2: мы удаляем этот узел из графа и добавляем его в список топологических порядков сортировки.

Шаг 3: Удалите те узлы, у которых есть исходящие ребра.

Шаг 4: Уменьшите степень вхождения на количество связанных ребер, которые были удалены.

Шаг 5: Повторяйте шаги 1–4, пока не останется узлов с нулевой степенью вхождения.

Шаг 6: Убедитесь, что все элементы расположены в правильной последовательности.

Шаг 7: Теперь мы отсортировали заказ из шага 6.

Шаг 8: Положите конец алгоритму.

 

Код Python : ниже приведена реализация приведенного выше примера на Python.

 

fromcollectionsimportdefaultdict

classbuildGraph :

def__init__(self, nodes : int) :
self.nodes= nodes

# Теперь мы сохраняем граф в формате смежного списка
self.adjListDetails=defaultdict(list)

# Он будет хранить информацию о входящих
ребрах определенного узла 

# в самом
self.count_numbers_of_incoming_edge_of_a_node= []

# Мы сохраняем отсортированные узлы в топологическом порядке
self.topological_sorted_order= []

# Мы храним информацию обо всех тех узлах, которые
# не имеют входящих ребер в графе
self.nodes_have_zero_incoming_edges= []

# Теперь мы создаем смежный список всех графов для сортировки
defAddGraphEdge (self, source :int, destination : int) :
self.adjListDetails[source].append(destination)
self.count_numbers_of_incoming_edge_of_a_node[destination] +=1

defTopologicalSortAlgorithm (self) :

for node inrange(self.nodes) :
ifself.count_numbers_of_incoming_edge_of_a_node[node] ==0 :
self.nodes_have_zero_incoming_edges.append(node)

whileself.nodes_have_zero_incoming_edges :
self.nodes_have_zero_incoming_edges.sort()
            source =self.nodes_have_zero_incoming_edges.pop(0)

# итерация по соседнему списку
if source inself.adjListDetails :
for node inself.adjListDetails[source] :
self.count_numbers_of_incoming_edge_of_a_node[node] -=1
ifself.count_numbers_of_incoming_edge_of_a_node[node] ==0 :
self.nodes_have_zero_incoming_edges.append(node)

self.topological_sorted_order.append(source)

print("Топологический порядок сортировки: "+str(self.topological_sorted_order))

defmain() :

number_of_nodes=7
    graph =buildGraph(number_of_nodes)
graph.count_numbers_of_incoming_edge_of_a_node= [0] *number_of_nodes

graph.AddGraphEdge(0,2)
graph.AddGraphEdge(0,5)
graph.AddGraphEdge(1,3)
graph.AddGraphEdge(1,6)
graph.AddGraphEdge(2,4)
graph.AddGraphEdge(3,5)
graph.AddGraphEdge(5,2)
graph.AddGraphEdge(5,4)
graph.AddGraphEdge(6,2)

graph.TopologicalSortAlgorithm()

if __name__ =="__main__" :
main()

 

 

Выход:

Топологический порядок сортировки: [0, 1, 3, 5, 6, 2, 4]

 

Временная сложность алгоритма топологической сортировки:

Общее время обработки алгоритма равно O (E + N), где E представляет количество ребер, а N представляет количество узлов в графе. Затем, на следующем шаге, мы должны вычислить степень входа каждого узла, что обычно занимает O(E) раз, а затем поместить все эти узлы в отсортированный список, где их степень входа равна нулю, что занимает O(N) раз. раз. Таким образом, общая временная сложность алгоритма топологической сортировки составляет O (E+N).

Но пространственная сложность алгоритма топологической сортировки составляет O (N), что равно общему количеству узлов в графе.

 

Применение:

1. Топологическая сортировка очень полезна для нахождения цикла графа.
2. Алгоритм топологической сортировки используется для определения условий взаимоблокировки в операционной системе.
3. Алгоритм топологической сортировки используется для поиска кратчайшего пути во взвешенном ациклическом графе.

 

Вывод :

В этой статье мы узнали еще об одном важном алгоритме — топологической сортировке. Мы видели, что этот алгоритм работает только с ациклическими графами. Алгоритм топологической сортировки также помогает определить порядок составления задачи. Алгоритм топологической сортировки имеет много преимуществ в реальном времени, например поиск кратчайшего пути. Поскольку топологическая сортировка чрезвычайно полезна, каждый программист и студент должен хорошо понимать этот алгоритм.