Восстановление алгоритма деления для целого числа без знака

Эффективное выполнение операций деления является краеугольным камнем компьютерной арифметики и программирования. Алгоритм восстановления деления для целых чисел без знака — это метод, который позволяет компьютерам точно и быстро делить числа. В отличие от других алгоритмов деления, алгоритм восстановления деления не только выдает точные коэффициенты, но и минимизирует количество требуемых шагов. В этой статье рассматриваются тонкости алгоритма восстановления деления для целых чисел без знака, исследуются его принципы, этапы и преимущества. Независимо от того, являетесь ли вы энтузиастом компьютерных наук или программистом, стремящимся разобраться в алгоритмах деления, эта статья предоставляет исчерпывающее руководство по алгоритму восстановления деления.
Что такое алгоритм восстановления деления для целых чисел без знака?
Алгоритм восстановления деления — это метод, используемый для выполнения операций деления над целыми числами без знака в компьютерной арифметике. Он предназначен для эффективного вычисления частного и остатка при делении одного целого числа без знака (делимого) на другое (делитель), при этом также минимизируя количество вычислительных шагов.
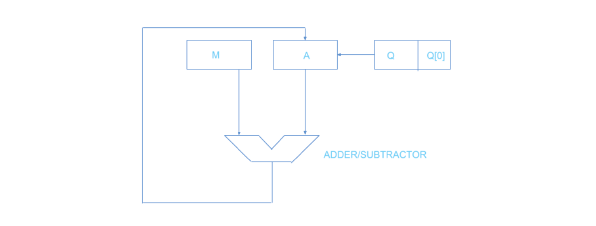
В этой статье будет использоваться процедура восстановления для целых чисел без знака. Термин «восстановление» относится к тому факту, что после каждого повторения восстанавливается значение регистра A.
Регистр Q в этом случае содержит частное, в то время как регистр A содержит остаток. Здесь делитель загружается в M, а n-разрядное делимое загружается в Q. Регистр, значение которого восстанавливается после итерации и для которого он назван Восстанавливающим, изначально хранится равным 0.
Давайте обсудим шаги один за другим:
Шаги по восстановлению алгоритма деления для целого числа без знака
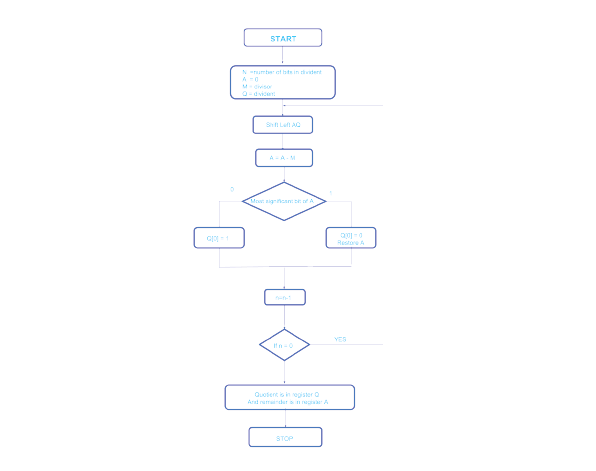
Шаг 1: Инициируйте процесс, установив в регистрах соответствующие значения, где Q представляет делимое, M обозначает делитель, A начинается с 0, а n обозначает количество битов в делимом.
Шаг 2: Переместите содержимое регистров A и Q влево, рассматривая их как единую единицу.
Шаг 3: Выполните вычитание, вычтя содержимое регистра M из A, и сохраните результат обратно в A.
Шаг 4: Проверьте старший бит A. Если он равен 0, установите младший значащий бит Q равным 1. И наоборот, если старший значащий бит равен 1, установите младший значащий бит Q равным 0. Кроме того, восстановите значение регистра A в его состояние перед вычитанием с помощью M.
Шаг 5: Уменьшите значение счетчика n на единицу.
Шаг 6: Проверьте, достигло ли значение n нуля. Если нет, вернитесь к шагу 2 и повторите процесс.
Шаг 7: Наконец, процесс деления завершается, частное находится в регистре Q, в то время как регистр A содержит остаток.
Давайте обсудим эти шаги для восстановления алгоритма деления для целого числа без знака на примере.
Пример восстановления алгоритма деления для целого числа без знака
Выполнить алгоритм восстановления деления
| n | M | A | Q | Операция |
|---|---|---|---|---|
| 4 | 00011 | 00000 | 1011 | инициализировать |
| 00011 | 00001 | 011_ | сдвиг влево AQ | |
| 00011 | 11110 | 011_ | A= A-M | |
| 00011 | 00001 | 0110 | Q[0]=0 И восстанавливаем A | |
| 3 | 00011 | 00010 | 110_ | сдвиг влево AQ |
| 00011 | 11111 | 110_ | A= A-M | |
| 00011 | 00010 | 1100 | Q [0]= 0 | |
| 2 | 00011 | 00101 | 100_ | сдвиг влево AQ |
| 00011 | 00010 | 100_ | A= A-M | |
| 00011 | 00010 | 1001 | Q [0]= 1 | |
| 1 | 00011 | 00101 | 001_ | сдвиг влево AQ |
| 00011 | 00010 | 001_ | A= A-M | |
| 00011 | 00010 | 0011 | Q [0]= 1 |
Не забудьте увеличить значение старшего бита A, равное 1, или 1. Регистр Q содержит частное, то есть 3, в то время как регистр A содержит оставшуюся часть значения, то есть 2.
Заключение
Алгоритм восстановления деления является эффективным и точным методом выполнения операций деления для целых чисел без знака. Сочетая принципы вычитания, сдвига и сравнения, этот алгоритм достигает точных результатов при минимизации вычислительных шагов. Его пригодность для аппаратной реализации и его роль в различных компьютерных архитектурах подчеркивают его важность в современных вычислениях. Знакомясь с областью алгоритмов деления, помните, что алгоритм восстановления деления является свидетельством изобретательности и оптимизации, присущих компьютерной арифметике.
Часто задаваемые вопросы по восстановлению алгоритма деления для целого числа без знака
Вот несколько часто задаваемых вопросов по восстановлению алгоритма деления для целого числа без знака.
Вопрос 1. Чем алгоритм восстановления деления отличается от других алгоритмов деления?
Алгоритм восстановления деления выделяется своей способностью обеспечивать как точное частное, так и эффективное выполнение. В отличие от некоторых алгоритмов, требующих итеративной коррекции, восстановление деления вычисляет частное при минимизации количества операций.
Вопрос 2: Как работает алгоритм восстановления деления?
Алгоритм включает в себя итеративное вычитание делителя из делимого при одновременном сдвиге как частного, так и остатка влево. Если результат вычитания отрицательный, значение восстанавливается путем обратного сложения делителя. Этот процесс продолжается до тех пор, пока делимое не станет неотрицательным.
Вопрос 3: Каковы преимущества использования алгоритма восстановления деления?
Преимущества алгоритма восстановления деления заключаются в его способности выдавать точные коэффициенты, относительно малом количестве итераций и совместимости с аппаратной реализацией. Эти факторы делают его подходящим для быстрых и эффективных операций деления.
Вопрос 4: Существуют ли какие-либо ограничения или сценарии, в которых алгоритм может быть неоптимальным?
Эффективность алгоритма восстановления деления снижается при делении очень больших чисел по мере увеличения числа итераций. В таких случаях могут быть более подходящими другие алгоритмы деления, такие как невосстанавливающее деление.
Вопрос 5: Как получается частное в алгоритме восстановления деления?
Частное накапливается во время итераций путем сдвига и добавления 1 при выполнении восстановления. В конце алгоритма значение, накопленное в регистре частных, представляет собой конечное частное.
Вопрос 6: Обрабатывает ли алгоритм восстановления деления остатки?
Да, остаток — это значение, оставшееся в регистре деления в конце алгоритма. Оно представляет часть, которая не может быть равномерно разделена делителем.
Вопрос 7: Используется ли алгоритм восстановления деления в современных вычислениях?
Хотя современные процессоры часто используют более совершенные алгоритмы, принципы алгоритма восстановления деления все еще влияют на операции деления. Его понимание остается важным для компьютерных архитекторов и программистов низкого уровня.
Вопрос 8: Можно ли применить алгоритм восстановления деления к делению с плавающей запятой?
Алгоритм восстановления деления в основном предназначен для деления целых чисел. Для деления с плавающей запятой необходимы более сложные алгоритмы для учета дробных частей.
Редактор: AndreyEx