Иерархия Хомского в теории вычислений

Иерархия Хомского в теории вычислений, названная в честь известного лингвиста и когнитивиста Ноама Хомского, является фундаментальной концепцией в области теоретической информатики. Она классифицирует формальные грамматики и языки на четыре различных уровня, каждый из которых обладает возрастающей выразительной силой. Эта иерархия дает ценную информацию о возможностях и ограничениях вычислительных моделей, проливая свет на природу самих вычислений.

Введение в формальные грамматики и языки

Формальные грамматики служат основой для точного и систематического описания структуры языков. Они состоят из набора правил, которые определяют, как могут генерироваться строки символов. В этом контексте язык относится к набору строк, составленных из заданного алфавита, который представляет собой конечный набор символов.

Четыре уровня иерархии Хомского в TOC

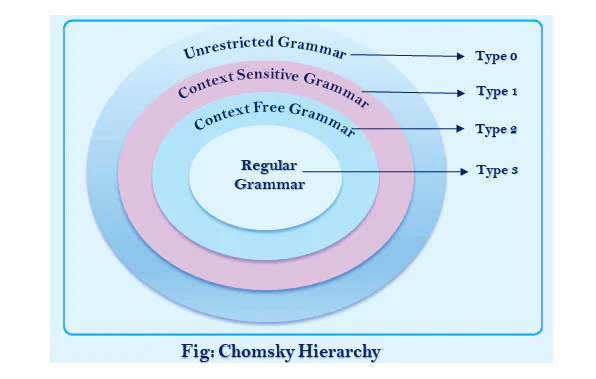
Иерархия Хомского в TOC состоит из четырех уровней, организованных в порядке возрастания сложности и генерирующей способности

a. Тип 3: регулярные языки

На самом низком уровне иерархии у нас есть регулярные языки. Эти языки могут быть описаны с помощью регулярных выражений или распознаны конечными автоматами. Обычные языки имеют простые правила распознавания образов и подходят для таких задач, как лексический анализ в языках программирования.

b. Тип 2: контекстно-свободные языки

Контекстно-свободные языки находятся на один уровень выше в иерархии. Их можно описать с помощью контекстно-свободных грамматик. Эти грамматики состоят из правил, которые определяют, как нетерминальные символы могут быть заменены последовательностями терминальных и нетерминальных символов. Контекстно-свободные языки обычно используются для определения синтаксиса языков программирования и распознаются автоматами pushdown.

c. Тип 1: контекстно-зависимые языки

Контекстно-зависимые языки расширяют выразительные возможности контекстно-свободных языков, позволяя использовать правила, учитывающие контекст, в котором появляются символы. Этот уровень иерархии распознается линейно-ограниченными автоматами, которые имеют ограниченное пространство на ленте для вычислений. Контекстно-зависимые языки фиксируют определенные лингвистические конструкции, которые недоступны контекстно-свободным грамматикам.

d. Тип 0: Рекурсивно перечислимые языки

На самом высоком уровне иерархии Хомского в TOC у нас есть рекурсивно перечислимые языки. Эти языки могут быть сгенерированы неограниченными грамматиками или распознаны машинами Тьюринга. Рекурсивно перечислимые языки охватывают все возможные языки, которые могут быть вычислены, что делает их самым мощным классом в иерархии. Однако эта мощь достигается ценой неразрешимости и невычислимости для многих задач.

Последствия и значение иерархии Хомского в теории вычислений

Иерархия Хомского в TOC имеет глубокие последствия для теории вычислений и лингвистики:

a. Вычислительная сложность: По мере продвижения вверх по иерархии сложность распознавания языков возрастает. Обычные языки могут быть распознаны за линейное время, контекстно-свободные языки — за полиномиальное время, а контекстно-зависимые языки — за недетерминированное полиномиальное время. Распознавание рекурсивно перечислимых языков может занимать бесконечное количество времени, в зависимости от конкретной конфигурации машины Тьюринга.

б. Классификация языков: Иерархия позволяет нам классифицировать языки на основе их порождающей способности. Эта классификация актуальна не только для информатики, но и для лингвистики. Естественные языки, такие как английский или испанский, как правило, более выразительны, чем формальные языки, описываемые обычными или контекстно-свободными грамматиками.

c. Пределы вычислений: Иерархия Хомского в TOC устанавливает пределы того, что может быть вычислено в рамках различных вычислительных моделей. Например, некоторые проблемы по своей сути выходят за рамки контекстно-свободных грамматик или даже машин Тьюринга. Это понимание имеет прямое применение при разработке алгоритмов, анализе сложности и изучении неразрешимости.

Заключение

Иерархия Хомского в TOC является фундаментальной основой для понимания возможностей и ограничений вычислительных моделей. Ее разделение формальных грамматик и языков на четыре различных уровня обеспечивает структурированный взгляд на сложность распознавания и генерации языков. От регулярных выражений, используемых в текстовом поиске, до сложности синтаксиса языка программирования — влияние иерархии Хомского в TOC является всеобъемлющим и поучительным, формируя наше понимание границ и возможностей вычислений.

Часто задаваемые вопросы (FAQs)

Вот несколько часто задаваемых вопросов по иерархии Хомского в TOC.

Вопрос 1. Что такое иерархия Хомского?

Иерархия Хомского — это система классификации, которая подразделяет формальные грамматики и языки на четыре уровня в зависимости от их сложности и порождающей способности. Эти уровни варьируются от обычных языков (простые шаблоны) до рекурсивно перечислимых языков (бесконечные вычисления), обеспечивая понимание возможностей и ограничений вычислительных моделей.

Вопрос 2. Как иерархия Хомского соотносится с языками программирования?

Иерархия Хомского имеет отношение к языкам программирования, поскольку помогает определить и понять их синтаксис. Контекстно-свободные языки, второй уровень иерархии, обычно используются для описания грамматик языков программирования. Это помогает в разработке компиляторов, интерпретаторов и синтаксических анализаторов, обеспечивающих точный синтаксический анализ языка и перевод.

Вопрос 3. Можете ли вы привести реальные примеры языков с каждого уровня иерархии?

Вот несколько примеров из реального мира:

• Обычный язык: набор всех строк, содержащих четное число ‘0’ и ‘1′.
• Контекстно-свободный язык: язык хорошо сформированных арифметических выражений.
• Язык контекста: естественные языки, такие как английский или испанский, которые имеют сложные грамматические правила, зависящие от контекста.
• Рекурсивно перечислимый язык: набор всех допустимых описаний машины Тьюринга, которые останавливаются при вводе ‘0’.

Вопрос 4. Каково значение иерархии Хомского в лингвистике?

Иерархия Хомского оказала глубокое влияние на лингвистику. Она демонстрирует формальную иерархию языковой сложности, помогая лингвистам понять структурные различия между различными языками. Более того, она разъясняет присущие формальным языкам ограничения в отражении всей сложности естественных языков, таких как английский или французский.

Вопрос 5. Существуют ли практические следствия иерархии Хомского за пределами теории?

Идеи иерархии имеют практическое значение для всей информатики. Она помогает разрабатывать эффективные алгоритмы для синтаксического анализа и распознавания языков, обеспечивая корректную работу компиляторов и интерпретаторов. Кроме того, иерархия устанавливает пределы вычислений, выделяя проблемы, которые принципиально неразрешимы с помощью определенных вычислительных моделей, что имеет решающее значение для понимания алгоритмической сложности и границ вычислимости.

(1 оценок, среднее: 1,00 из 5)

Загрузка...